データサイエンティストのたまご育成日記 vol.13 －最適化問題を学んだお話－

みなさん、こんにちは！デジタルテクノロジー統括部に新卒入社した長谷川智彦です。データサイエンティスト未経験の新卒社員がデジタルテクノロジー統括部でどんなことをやっているのか、どのように成長していくのかの学びの過程を記録していくこの企画。今回は最適化問題（数理最適化問題）で勉強したことについて書いていきます。

最適化問題とは？
pulpライブラリについて
総括

もうすぐ1年が経ってしまいますね、1年前は修士論文に追われていたのが懐かしいです。現在は3~4つのプロジェクトに加えていただきながら、分析を行ったり分析に必要なデータを揃えたりする作業をメインで行っています。今回はそのうちの1つのプロジェクトで一部に活用されていた最適化のロジックとpythonのpulpライブラリに関して学んだことについて書いていきます。

最適化問題とは？

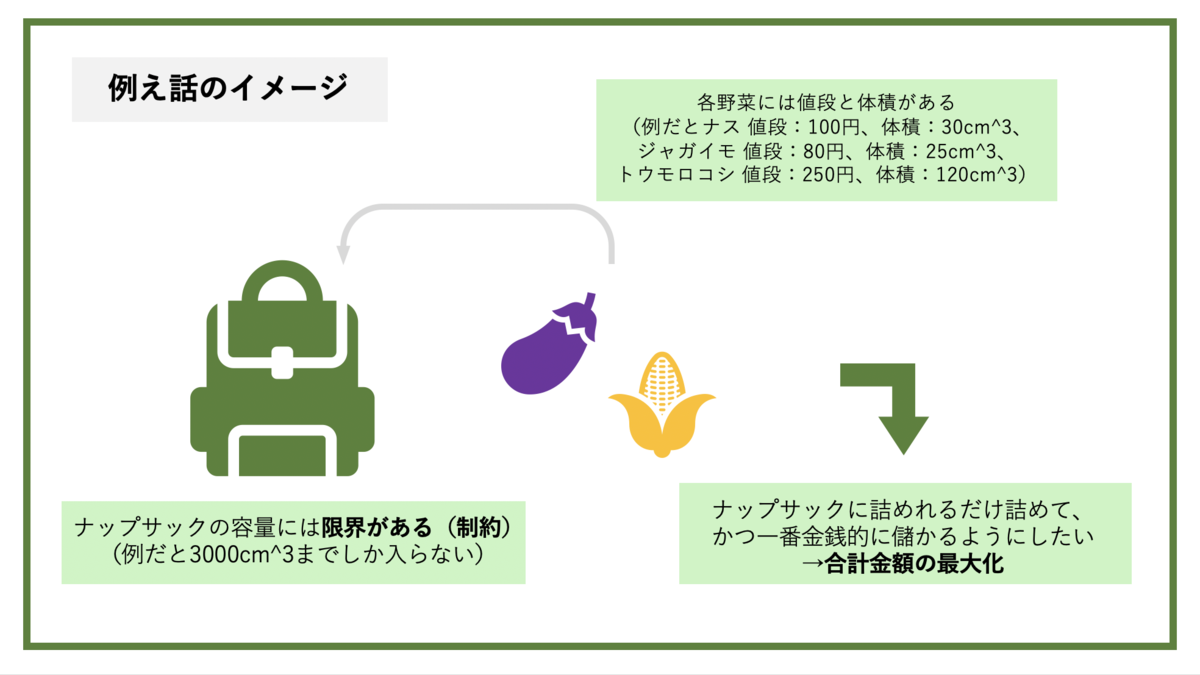
いきなり最適化問題と書いたのですが最適化問題とはなんぞや？と初めの僕はなりました。最適化問題とは何かを調べてみると、最適化問題とは制約条件がある下で、目的関数を最大または最小にする解の組み合わせを求める問題だそうです。個人的にはこれでもまだわかりづらいと感じるので、最適化問題で有名なナップサック問題を引用した例え話で説明したいと思います。

皆さんナップサックを1つイメージしてください。とあるスーパーで野菜の大特価セールが行われており、なんとナップサックに入るだけ野菜を詰めても一律1000円というのです（この1000円は今回関係ないです）。皆さんの中にはできるだけ詰めて野菜の元値で考えた場合に一番詰めた野菜の合計金額が最大になるように詰めようと考える方もいるかと思います。ただ、皆さんすぐにイメージしてもらえると思うのですが、ナップサックの容量には限界があります。一方、野菜においては元々の値段と体積が各野菜によって決まっています。ここで考えるのが詰めた野菜の体積の合計がナップサックの体積を超えない範囲で詰めた野菜の合計金額が最大になるようにすれば一番お得です（金銭的に）。

これを数式に落としてみます。ナップサックの容量の最大を3000cm^3、野菜としてナス（値段：100円、体積：30cm^3）、ジャガイモ（値段：80円、体積：25cm^3）、トウモロコシ（値段：250円、体積：120cm^3）と設定します。ナスの個数をx、ジャガイモの個数をy、トウモロコシの個数をzと設定すると以下のようになります（ちなみに野菜はそれぞれ必ず1個は買うとします）。

\\ 例え話を数式に落としたら //
max 100*x + 80*y + 250*z　（最大化する目的関数）
30*x + 25*y + 120*z ≦ 3000　（野菜の合計体積がナップサックの体積を超えない）
x ≧ 1
y ≧ 1
z ≧ 1

上記の式の100*x + 80*y + 250*z（＊は掛け算を表します）が野菜の合計金額を表すのですが、これが最大となる各野菜の個数（x、y、z）をナップサックの限界（3000cm^3）を超えない制約の中で求めるのが最適化問題になります。最適化問題では不等号（＜や＞）が制約を表現してくれています。

この最適化問題ですが、高校で数学Ⅱの授業を受けていた方は実はすでに触れています。この問題を覚えているでしょうか

あ〜、あった気もするという方もいらっしゃると思います。高校の時の僕はまさか十数年後に仕事でまた出会うとは思っていませんでしたが、知らない間に（僕が授業中うたた寝してたのですが）最適化の問題に触れていたんですね、高校生の皆さん勉強に意味はありました。

pulpライブラリについて

さっと最適化問題に関して説明させていただきましたが、Pythonには最適化問題を解くためのpulpライブラリが存在します（pulpには無料、有料含め何個かのソルバーがあるみたいです。今回はCOINプロジェクトの無料ソルバーを使用します）。
以下からは最適化問題の他の例を挙げながらpulpライブラリを使って最適化問題を解いてみたいと思います。

さて、チーム構成に関して最適化問題を作ってみたいと思います。

ある会社で新しいアプリを作成することになりました。
新人のはせがわくんは部長からこんなことを言われたとします。
部長「人件費500万以内で1ヶ月でアプリのプロトタイプを作ってくれない？」
新人はせがわくんは部長から任されたことなので張り切りながら、アプリのプロトタイプ（試作品）を作るのに必要な人員や人員数を調べるとエンジニア2人とデザイナー1人が最低限必要であること、エンジニアの給料は1ヶ月で80万円、デザイナーの給料は1ヶ月で65万円、部内にはエンジニアが10人、デザイナーが5人在籍していることがわかりました（例え話なので、いやそれでは無理だなどご意見あるかと思いますがスルーしてください）。
はせがわくんは節約の概念が吹っ飛んでいるのでせっかく500万の予算をもらったなら使えるギリギリまで使って最大人数を借りようと考え、予算内でエンジニアとデザイナーを何人働いてもらえるか最適化問題を解くことで知ろうとしました。

なかなか、無理やりな設定にしましたが、最適化問題では予算や在庫数など資源に制限がある時などに応用されています、関わっているプロジェクトでは適切に配信するためにメールの配信のロジックの一部に使用していました。

上記の設定を最適化問題に落とし込んだときの数式とpulpライブラリを使用した時のPythonコードを以下に示します。

【数式】
max x + y
700000*x + 650000*y ≦ 5000000
10 ≧ x ≧ 2
5 ≧ y ≧ 1

【Pythonコード】

#ライブラリのインポート
import pulp

#目的関数の設定と変数の設定
problem = pulp.LpProblem('sample', pulp.LpMaximize)
a = pulp.LpVariable('a',0,10)
b = pulp.LpVariable('b',0,5)

#制約条件の記述
problem += a >= 2
problem += b >= 1
problem += 700000*a + 650000*b <= 5000000

status = problem.solve()
print("Status", pulp.LpStatus[status])

print(problem)

print("result")
print("a",a.value())
print("b",b.value())

## 結果 a=2.5 b=5.0になります。

pulpライブラリを使って予算ギリギリまで使った場合の最適人数がわかりました、このようにPythonを使って比較的簡単に最適化問題を解くことができます。興味ある方は是非試してみてください（Excelでも最適化問題を解くためのソルバーが存在するので、コードはちょっと、、、という方も必要に迫られたら調べてみてください）。