
本記事は、データ分析技術(巡回セールスマン問題)の応用可能性を検証する技術ブログ記事であり、東京ディズニーランド®の攻略法やアトラクション利用を推奨するものではありません。パーク内での行動については、株式会社オリエンタルランドが定める公式のルールとマナーを必ず遵守してください。 本記事に記載された内容は、株式会社オリエンタルランドおよびウォルト・ディズニー・カンパニー(ディズニー社)の公式見解や情報とは一切関係ありません。
はじめに: 巨大テーマパークvsデータアナリスト
こんにちは。アドベントカレンダー12日目担当の小澤です。 パーソルキャリアのAIプロダクトソリューション部に所属し、リードデータアナリストとして機械学習モデル開発などに携わっております。
さて、突然ですが皆さん、ディズニーランドは好きですか?夢と魔法の王国、素敵ですよね。お子様に夢の国行きをねだられる方も多いのではないかと推察します。ですが、同時にこう思ったことはないでしょうか?
「とにかく広い!」「一日じゃ全然回りきれない!」
「スプラッシュ・マウンテン」に乗った直後に「ビッグサンダー・マウンテン」が空いたと聞いて向かい、その後「モンスターズ・インク"ライド&ゴーシーク!"」に行ったら、また端から端への大移動。そんな経験、ありませんか?特に、お子様連れの皆様。お子様の無限にも思える体力に、苦労することも多いのではないでしょうか。
なぜこの記事を書こうと思ったか
ファンとしては、できるだけ多くのアトラクションや名所を体験したい。それが人情でしょう。しかし、あの広大な敷地を効率よく回る計画を「勘」や「経験」だけで立てるのは至難の業です。
ここで、データアナリストとしてはこう考えます。
- 「この『パーク内の非効率な移動』を、最適化できるのではないか?」
- 「普段の業務で『タスクの実行順序』を考えるように、ディズニーランドの回り順も最適化できるはずだ」
そう、データアナリストとは、非効率を見過ごせず、すべてをデータとして捉え、最短・最適ルートを計算したくなる生き物なのです。(※個人の見解です) 「ディズニーランド」という最強のテーマパークに対し、「データアナリスト」がガチで効率化(最適化)を挑んだらどうなるのか? これが、今回この記事を書こうと思った最大の動機です。
この記事でやること
この記事では、ディズニーランドの主要な名所(アトラクションなど)を全て巡ることを想定し、 「理論上、最も移動効率の良い(最短の)巡回ルート」を計算します。
この計算のために使うのが、古くから知られる有名なアルゴリズム「TSP(巡回セールスマン問題)」です。
本記事は、データアナリストが夢の国をどうデータ化し、どう解いたかの奮闘記です。 (※あくまで移動距離や移動時間に基づいた「机上の計算」です。)
TSP(巡回セールスマン問題)とは?をサクッと解説
どんな問題か?
先ずは巡回セールスマン問題(Traveling Salesman Problem, 以降TSPと呼称)について簡単に解説します。
TSPとは、複数の拠点と拠点間の移動コスト(金額や時間など…)を与えられた際、全ての拠点を一度ずつ巡り、かつ最初の拠点に戻ってくるルートの中で、コスト最小のルートを求める問題です。例えば、以下のような拠点が設置されていれば、
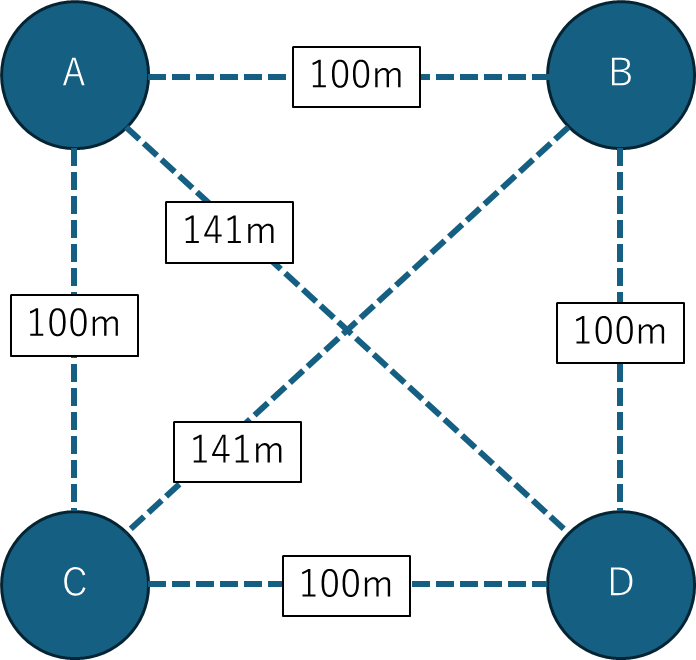
以下のように移動するのがベストである、ということです。
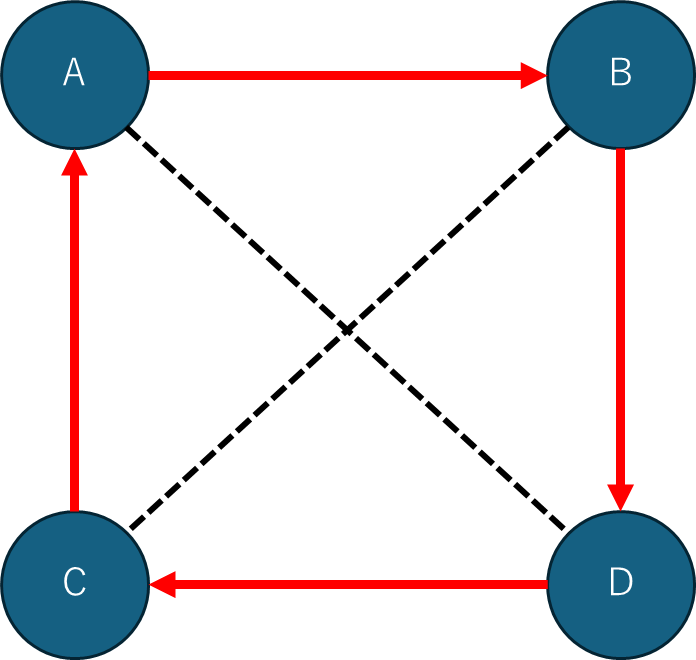
拠点の数が少ない時は直感的に分かりますが、拠点の数が増えてくると、スパコンでも太刀打ちできない強烈な問題になります。 拠点数がnの時、$(n-1)!$通りのルートが考えられます。今回の例では4拠点なので、6通りのルートを総当たりすれば良いです。 これがもし6拠点になった場合、120通りのルートに、10拠点になっただけで、362880通りと、ルートの数が加速度的に増えていきます。
なぜこれをテーマパーク巡りに応用できるのか
さて、この「巡回セールスマン問題」が、なぜ今回のディズニーランド攻略に応用できるのか。もうお分かりの方も多いかもしれません。 先ほどのTSPの構成要素を、ディズニーランドに当てはめてみましょう。
- TSPにおける「拠点」
- ディズニーランドの「各アトラクション」や「名所」(例:スペース・マウンテン、シンデレラ城、ビッグサンダー・マウンテン…)
- TSPにおける「移動コスト」
- 各名所の間を移動するための「徒歩での移動時間」または「移動距離」
- TSPが求める「コスト最小のルート」
- 総移動時間が最短となる、パークの巡回ルート
このように、完璧に読み替えることができます。つまり、データアナリストの視点から見ると、
「ディズニーランドの主要な名所をすべて巡る、最も効率的な(移動時間が短い)順番は何か?」
という問題は、
「各アトラクション(拠点)間の移動時間(コスト)が分かっている時、全アトラクションを巡る最短ルート(解)を求める問題」
となり、これはまさに「巡回セールスマン問題(TSP)」そのものなのです。
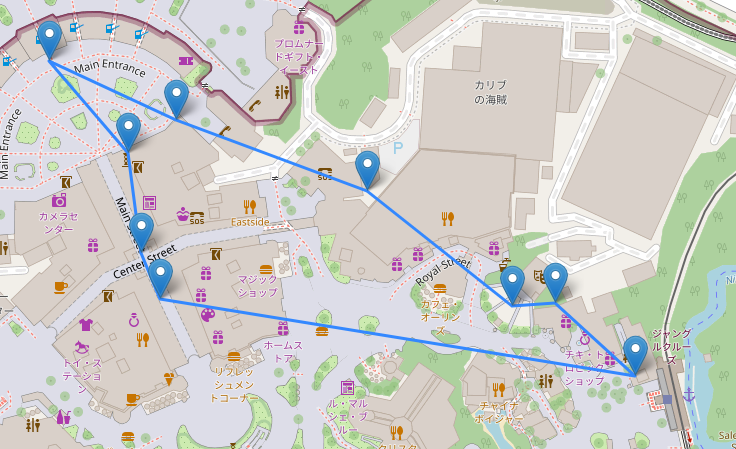
夢と魔法の王国を、このように「点(ノード)」と「コスト(エッジ)」の集合としてデータ化し、最適化計算にかける。 それが今回のアプローチです。 次の章では、実際にどのようにしてディズニーランドを「データ」にし、TSPとして解いたのか、その具体的なステップをご紹介します。
テーマパークをデータにして解く
Step1: 問題設定
ディズニーランドの「名所」と「アトラクションの入り口」を全て一度ずつ周り、一番短い経路を探す
Step2: ランドを「地図」にする
Google Mapsで名所やアトラクションの入り口を探し、緯度経度を取得。 その名所の名前、英語名、緯度経度をメモし、データを作成する

実はピン止めした後に右クリックすると、緯度経度をコピー出来ます。

合計65か所の拠点を抽出しました。
Step3: 各拠点間の「コスト」を計算する
各拠点間のコストは、今回は単純に緯度経度から計算します。(Haversineの公式)

Step4: TSPとして解く
TSPの解法は色々ありますが、現時点では3つの手法を試してみました
- 遺伝的アルゴリズム
- データ(解の候補)を遺伝子で表現した「個体」を複数用意し、適応度の高い個体を優先的に選択して交叉・突然変異などの操作を繰り返しながら解を探索する。
- 島モデル
- 複数の母集団を用いて各集団内で遺伝的アルゴリズムを実行し、定期的に個体の交換を行う
- 整数計画法
- 最適化問題において変数が整数値を取る必要がある問題を解決するための数学的手法
結果と考察
| 手法 | 結果[m] | 計算時間[s] |
|---|---|---|
| 遺伝的アルゴリズム | 3428.81 | 8.5 |
| 島モデル | 3136.19 | 90.2 |
| 整数計画法 | 3136.19 | 27.6 |
遺伝的アルゴリズムは計算時間は短いものの、あまり良くない結果が出ていますね。 実際に可視化してみると、以下のような状況です。全体的に少し遠回りしている印象を受けます。
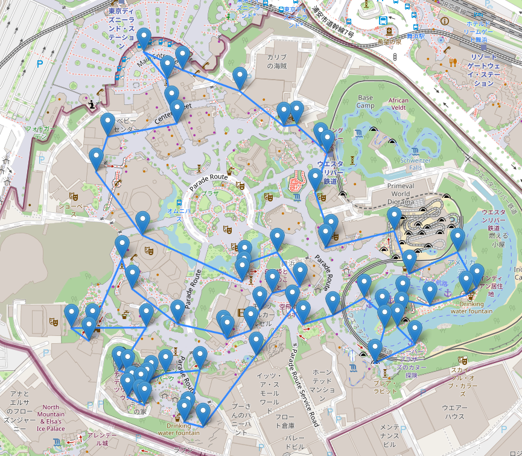
また、トゥーンタウン周りで交叉が発生してしまっていますね。
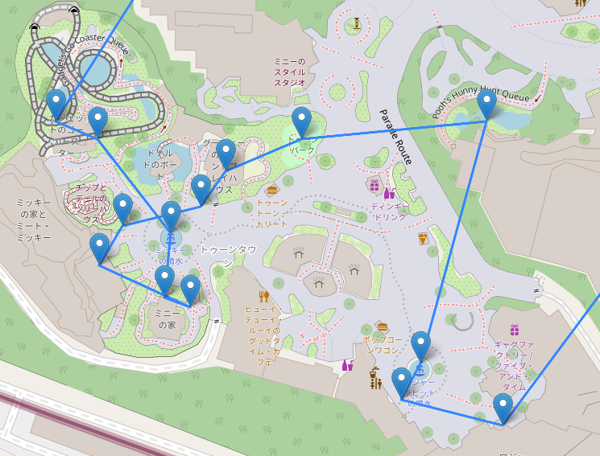
結果: 「理論上」の最短ルート
一方、島モデルと整数計画法は、どちらも「3136.19m」という同じ結果(最適解)を導き出しました。
- 島モデルはヒューリスティックスな手法(※厳密な最適解を保証しないが、良い解を高速に見つける手法)ですが、今回はパラメータを調整した結果、運良く最適解にたどり着きました。
- 整数計画法は、厳密に最適解を求める手法です。計算時間は島モデルより速いですね。
この最適ルートを可視化してみると、遺伝的アルゴリズムの結果と比べて明らかにスリムで、無駄のない経路になっているのが分かります。
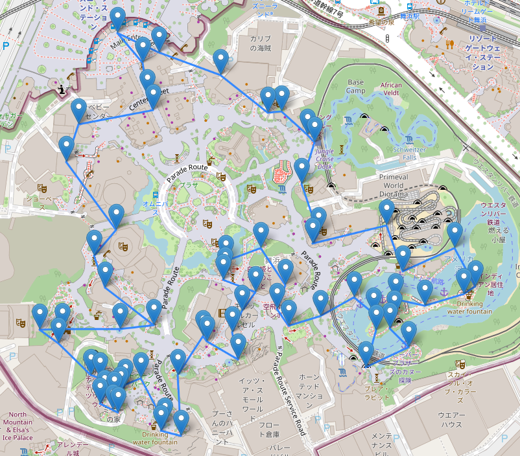
先ほど交叉していたトゥーンタウン周辺も、しっかりした経路になっています。
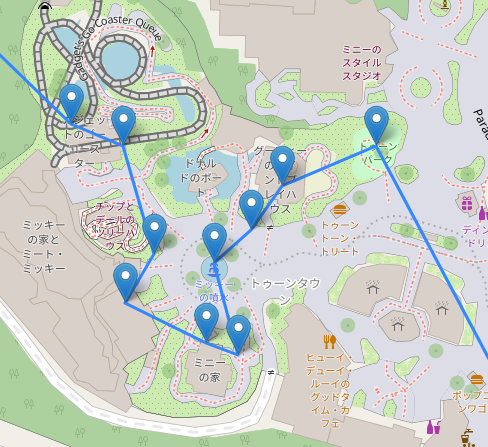
というわけで、理論上の最短ルートは「3136.19メートル」と判明しました! なんと、わずか3km強の移動で、あの広大なディズニーランドの主要65ヶ所をすべて巡れてしまう計算です。
考察: 本当に周れる?
…と、ここまで数理最適化の華々しい結果をお見せしてきましたが、実際にはこのルートは使い物になりません。
理由は単純に、「通れない場所をルートに含んでいるから」です。
これはStep3の「コスト計算」を、緯度経度間の直線距離(Haversineの公式)で行ったことが原因です。 計算上は最短でも、そこが道であるかどうかは一切考慮していません。
例えば、ウエスタンランド周辺ではアメリカ河を横切っていたり、

他にも、ピーターパン空の旅周辺では明らかに建物を突き抜けています。

以上のことから、この「理論上の最短ルート」は、空を飛べるか、 壁をすり抜けられる特殊能力を持っていない限り、実行不可能であるという結論に至りました。
最後に
さて、「巨大テーマパーク vs データアナリスト」の戦いの結果は… ご覧の通り、ディズニーランドの完勝となりました。
「理論上の最短ルート」は、「池を渡り、建物を突き抜ける」という、物理法則を完全に無視したルートでした。 夢の国は、緯度経度と直線距離という単純なデータ(と数理最適化)で攻略できるほど、甘い相手ではありませんでした。 いやぁ、TSPは奥が深いです。
今回の敗因は明確です。もし、本当に「使い物になる」最強ルートをデータで導き出すなら、以下のアプローチが必要になるでしょう。
- コストの再定義: 直線距離(Haversine)ではなく、Google Maps APIなどを使い、実際の「道のり(徒歩時間)」をコストとして取得する。
- 制約の追加: 「アトラクションの待ち時間」という最大の変動要因を考慮に入れる。(これはTSPではなく、VRP(配送計画問題)に近い、さらに複雑な問題になります)
- 問題の分割: 「全65ヶ所制覇」ではなく、「人気アトラクション10選」や「午前中だけで回るファンタジーランド」など、問題を現実的に小さくして解く。
夢の国への挑戦は、まだまだ分析の余地がありそうです。
今回は「理論」を提供する形となりましたが、データアナリストの奮闘記として楽しんでいただけたなら幸いです。
以上、お付き合いいただきありがとうございました。 ぜひ、アドベントカレンダーの次の記事もお楽しみください。

小澤 陽介
データ・AIソリューション本部 AIプロダクトソリューション部 AIプロダクトソリューション1グループ
前々職は半導体製造会社にて、リソグラフィ工程のプロセスエンジニアリングに従事。前職では機械系メーカーR&Dにて数理最適化のアプリケーション開発及び工程可視化に従事。パーソルキャリアに入ってからはアナリストとして、主に生成系AIに関連するアプリケーション開発や検証に従事。意思決定の為の計算機開発にも携わっている。
※2025年12月現在の情報です。
