データサイエンティストのたまご育成日記 Vol.8 －データ分析研修回帰編－後編

みなさん、こんにちは。デジタルテクノロジー統括部に新卒入社した長谷川智彦です。
データサイエンティスト未経験の新卒社員がデジタルテクノロジー統括部でどんなことをやっているのか、どのように成長していくのかの学びの過程を記録していくこの企画。今回は前回の記事から行っている回帰問題の分析の続きである、モデルの構築と評価に関して書いていきます！

モデルの構築をやってみた

前回の記事ではデータを整えるところまでを行いました。なのでここからはデータの探索を行おうと思ったのですが、全てを見ていると時間が足りないので、先にモデルの構築を行い、モデルで重要とされる変数に絞った後に重要そうな変数だけ見ることにしました。
今回モデル構築で検討したのは以下の3つです。

\\ 選択したモデル //
重回帰分析＋変数減少法
Lasso回帰
LightGBMRegressor

それではまず重回帰分析＋変数減少法を見ていきます。
重回帰分析では初めに全ての変数のデータを放り込み、計算結果の係数と、各変数のp値を参照しながらp値が0.05以下のものだけを残していきました。（有意差のお話は今回省かせてもらいます。）
コードは以下の通りです。

#全てのダミー変数を代入
X2 = train_dummy_re.drop("SalePrice", axis=1)
＃今回の目的変数は住宅の価格（SalePrice）
y2 = train_dummy_re["SalePrice"]
X2 = sm.add_constant(X2)

X_dummy_re, X_test_dummy_re, y_dummy_re, y_test_dummy_re = train_test_split(X2, y2, train_size =0.5, random_state=0)
# 最小二乗法でモデル化
model2 = sm.OLS(y_dummy_re, X_dummy_re)
result = model2.fit()

# 重回帰分析の結果を表示する
result.summary()

以下が結果の表の一部です。赤四角の中の値で0.05以下の変数を残していきました（同じ操作を３回行って絞っています）。こうして目的変数である住宅の価格（SalePrice）に影響しそうな変数を残していきます。

結果として残った変数は後ほど他のモデルの結果と共に後ほどまとめます。
変数減少法で変数を絞った重回帰分析でのRMSE値とR^2値は以下のようになりました。

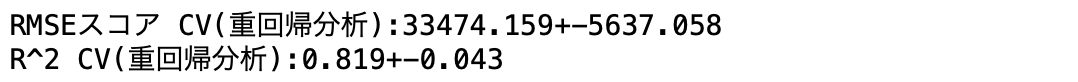
次にLasso回帰を行いました。Lasso回帰は正則化された線形回帰の1つで、残差平方和に重みのL1ノルムを足した関数（残差平方和＋L1正則化項）を、最小にすることで係数を決めていくのですが、詳しい説明はネットを探すと素晴らし解説がいっぱいあるのでそちらにお任せします。とりあえず、特徴としては外れ値があっても影響されにくくなっていること、目的変数の予測に重要でない変数の係数を０にしてくれることがあります。そう、０にしてくれるのです。つまり、簡単に考えれば重要な変数は残り、そうでない変数は係数が０になるので消えてくれるので重要な変数がすぐわかります。
ということで早速Lasso回帰を行ってみました。

from sklearn.linear_model import LassoCV

X2 = train_dummy_re.drop("SalePrice", axis=1)
y2 = train_dummy_re["SalePrice"]

#モデルのインスタンス化、cv＝５に設定
clf = LassoCV(eps=0.001, n_alphas=100, alphas=None, fit_intercept=True, normalize=False, precompute='auto', max_iter=5000, tol=0.0001, copy_X=True, cv=5, verbose=False, n_jobs=None, positive=False, random_state=None, selection='cyclic')

clf.fit(X2, y2)
pred = clf.predict(X2)
sq = np.sqrt(mean_squared_error(y2, pred))

print(clf.alpha_)
print(clf.coef_)
print(clf.intercept_)

print(sq)
print("R^2 CV(Lasso):{:.3f}".format(clf.score(X2,y2)))

実行したモデルでのRMSEと R^2値は以下のようになりました。

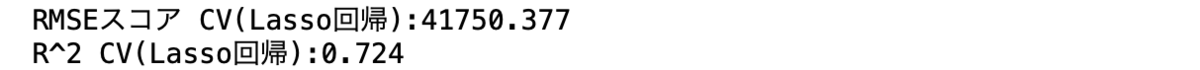
また今回のLasso回帰で目的変数である住宅価格に関係する変数の係数の大きさを可視化すると以下のようになります（正と負でそれぞれ上位10個を可視化しました）。

後ほど説明しますが、住宅の築年数（YearBuilt）や何かしらの面積（Areaとあるもの）が住宅価格に影響しそうです。

最後に最近Kaggleでかなりの人が使用しているLightGBMRegressorを使用して同様に交差検証を行い、RMSEとR^2を算出しました。
以下がコードになります。

#ライブラリのインポート
import lightgbm as lgb
from sklearn import datasets
from sklearn.metrics import accuracy_score
import numpy as np
import pandas as pd
import sklearn.preprocessing
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score
from sklearn.model_selection import KFold


＃LightGBMは決定木をベースにしているので LabelEncoder()を使用して質的変数を量的変数に変更しました。
train_re = pd.read_csv("train2.csv")
train_re = train_re.drop("Id", axis=1)
train_re = train_re.replace("NaN", np.nan)
train_re = train_re.replace("None", np.nan)
train_re[['MSSubClass','LotFrontage', 'LotArea','OverallQual', 'OverallCond', 'YearBuilt', 'YearRemodAdd','MasVnrArea','BsmtFinSF1','BsmtFinSF2', 'BsmtUnfSF', 'TotalBsmtSF','1stFlrSF', '2ndFlrSF', 'LowQualFinSF','GrLivArea', 'BsmtFullBath', 'BsmtHalfBath', 'FullBath', 'HalfBath','BedroomAbvGr', 'KitchenAbvGr', 'TotRmsAbvGrd','Fireplaces', 'GarageYrBlt', 'GarageCars', 'GarageArea','WoodDeckSF', 'OpenPorchSF', 'EnclosedPorch', '3SsnPorch','ScreenPorch', 'PoolArea', 'MiscVal','MoSold', 'YrSold', 'SalePrice']]=train_re[['MSSubClass','LotFrontage', 'LotArea','OverallQual', 'OverallCond', 'YearBuilt', 'YearRemodAdd','MasVnrArea','BsmtFinSF1','BsmtFinSF2', 'BsmtUnfSF', 'TotalBsmtSF','1stFlrSF', '2ndFlrSF', 'LowQualFinSF','GrLivArea', 'BsmtFullBath', 'BsmtHalfBath', 'FullBath', 'HalfBath','BedroomAbvGr', 'KitchenAbvGr', 'TotRmsAbvGrd','Fireplaces', 'GarageYrBlt', 'GarageCars', 'GarageArea','WoodDeckSF', 'OpenPorchSF', 'EnclosedPorch', '3SsnPorch','ScreenPorch', 'PoolArea', 'MiscVal','MoSold', 'YrSold', 'SalePrice']].fillna(0)
train_re[['MSZoning','Street', 'Alley','LotShape', 'LandContour', 'Utilities', 'LotConfig', 'LandSlope', 'Neighborhood', 'Condition1', 'Condition2', 'BldgType', 'HouseStyle','RoofStyle', 'RoofMatl', 'Exterior1st', 'Exterior2nd', 'MasVnrType', 'ExterQual', 'ExterCond', 'Foundation', 'BsmtQual', 'BsmtCond','BsmtExposure', 'BsmtFinType1', 'BsmtFinType2', 'Heating', 'HeatingQC','CentralAir', 'Electrical', 'KitchenQual', 'Functional', 'FireplaceQu', 'GarageType', 'GarageFinish', 'GarageQual', 'GarageCond', 'PavedDrive','PoolQC', 'Fence', 'MiscFeature','SaleType', 'SaleCondition']]=train_re[['MSZoning','Street', 'Alley','LotShape', 'LandContour', 'Utilities', 'LotConfig', 'LandSlope', 'Neighborhood', 'Condition1', 'Condition2', 'BldgType', 'HouseStyle','RoofStyle', 'RoofMatl', 'Exterior1st', 'Exterior2nd', 'MasVnrType', 'ExterQual', 'ExterCond', 'Foundation', 'BsmtQual', 'BsmtCond','BsmtExposure', 'BsmtFinType1', 'BsmtFinType2', 'Heating', 'HeatingQC','CentralAir', 'Electrical', 'KitchenQual', 'Functional', 'FireplaceQu', 'GarageType', 'GarageFinish', 'GarageQual', 'GarageCond', 'PavedDrive','PoolQC', 'Fence', 'MiscFeature','SaleType','SaleCondition']].fillna("-")
train_re["MasVnrArea"] = train_re["MasVnrArea"].astype("int64")
train_re["LotFrontage"] = train_re["LotFrontage"].astype("int64")
train_re["GarageYrBlt"] = train_re["GarageYrBlt"].astype("int64")


le = LabelEncoder()
for column in ['MSZoning','Street', 'Alley','LotShape', 'LandContour', 'Utilities', 'LotConfig', 'LandSlope', 'Neighborhood', 'Condition1', 'Condition2', 'BldgType', 'HouseStyle','RoofStyle', 'RoofMatl', 'Exterior1st', 'Exterior2nd', 'MasVnrType', 'ExterQual', 'ExterCond', 'Foundation', 'BsmtQual', 'BsmtCond','BsmtExposure', 'BsmtFinType1','BsmtFinType2', 'Heating', 'HeatingQC','CentralAir', 'Electrical', 'KitchenQual', 'Functional', 'FireplaceQu', 'GarageType', 'GarageFinish', 'GarageQual', 'GarageCond', 'PavedDrive','PoolQC', 'Fence', 'MiscFeature','SaleType', 'SaleCondition']:
le.fit(train_re[column])
train_re[column] = le.transform(train_re[column])

X_re = train_re.iloc[:,:-1]
y_re = train_re["SalePrice"]

＃計算結果を入れる空リストを作成
scores = []
r2_scores = []

＃交差検証
kf = KFold(n_splits=5, shuffle=True, random_state=0)
for tr_idx, va_idx in kf.split(X_re,y_re):
tr_x, va_x = X_re.iloc[tr_idx], X_re.iloc[va_idx]
tr_y, va_y = y_re.iloc[tr_idx], y_re.iloc[va_idx]
＃モデルのインスタンス化
model_cv = lgb.LGBMRegressor(boosting_type='gbdt', num_leaves=31, max_depth=- 1, learning_rate=0.001, n_estimators=10000, subsample_for_bin=200000, objective=None, class_weight=None, min_split_gain=0.0, min_child_weight=0.001, min_child_samples=20, subsample=1.0, subsample_freq=0, colsample_bytree=1.0, reg_alpha=0.0, reg_lambda=0.0, random_state=None, n_jobs=- 1, silent=True, importance_type='gain')
model_cv.fit(tr_x, tr_y, eval_set=[(va_x, va_y)],eval_metric= "rmse", verbose = 1000, early_stopping_rounds = 200)
va_pred = model_cv.predict(va_x)
score = np.sqrt(mean_squared_error(va_y, va_pred))
scores.append(score)
score2 = r2_score(va_y, va_pred) 
r2_scores.append(score2)
　＃分類時に寄与した変数のimportanceを表示
importance = pd.DataFrame(model_cv.feature_importances_, index = X_re.columns, columns=["importance"])
display(importance.sort_values("importance", ascending= False))

＃RMSEとR^2の値の記述
print("RMSEスコア CV(LightGBMRegressor):{:.3f}+-{:.3f}".format(np.array(scores).mean(),np.array(scores).std()))
print("R^2 CV(LightGBMRegressor):{:.3f}+-{:.3f}".format(np.array(r2_scores).mean(),np.array(r2_scores).std()))

まずRMSEとR^2値の結果としては以下のようになりました。

RMSEの単純な比較でいくとLightGBMRegressorが一番精度が高いモデルとなりました。Kaggleでの予測値の推測の際にはLightGBMRegressorを使用することにします。
次にそれぞれのモデルで目的変数に寄与した説明変数を見ていくと以下のようになりました。

重回帰：
'LotArea','OverallQual','OverallCond','YearBuilt','MasVnrArea','BsmtFinSF1','TotalBsmtSF','GrLivArea','BedroomAbvGr','KitchenAbvGr','GarageArea','Neighborhood_Crawfor','Neighborhood_NWAmes','Neighborhood_StoneBr','RoofMatl_WdShngl','PoolQC_Ex','PoolQC_Gd'
→築年数（YearBuilt）に加え、全体の品質（OverallQual,OverallCond）が値段に影響していそうです。他にも家のプールやキッチンなどの条件によっても変わりそうです。

Lasso回帰：
'YearBuilt','GarageArea','GrLivArea','TotalBsmtSF','MasVnrArea','OpenPorchSF','YearRemodAdd','BsmtFinSF1','WoodDeckSF','2ndFlrSF','MiscVal','GarageTrBlt'
→築年数(YearBuilt)や面積に関わりそうな変数（AreaやSFがある変数）が影響していそうです。

LightGBMRegressor:
'OverallQual','GrLivArea','GarageCars','TotalBsmtSF', 'BsmtFinSF1','LotArea','TotRmsAbvGrd','1stFlrSF','YearBuilt', 'YearRemodAdd', 'ExterQual','GarageArea','GarageType','Neighborhood','2ndFirSF'
→全体の品質や築年数、面積に関わりそうな変数が影響していそうです。

これらのモデルで共通してみられた変数を見てみると、
〈共通な変数〉
3つのモデルで共通→'YearBuilt','GarageArea','GrLivArea','TotalBsmtSF','BsmtFinSF1'
2つのモデルで共通→'OverallQual','MasVnrArea','Neighborhood','2ndFlrSF'
全体的に築年数や面積、品質に関係した変数が住宅価格に影響していそうなことがわかりました。個人的には Neighborhood(物理的に近くにあるもの？何を表しているのか具体的にはピンときませんでした)が影響しているのが興味深かったです。
影響しそうな変数がわかったのでより詳細に情報を得ていくために次の変数のグラフを作成しました。
グラフを作成した変数：築年数（'YearBuilt'）、面積（いくつのあるので代表として'GarageArea','GrLivArea'）、品質（'OverallQual'）、また個々の家の設備（代表として'PoolQC'、'RoofMatl'）、Neighborhood

ではまず築年数と住宅価格の関係から見ていきます。
〈築年数と住宅価格の関係〉

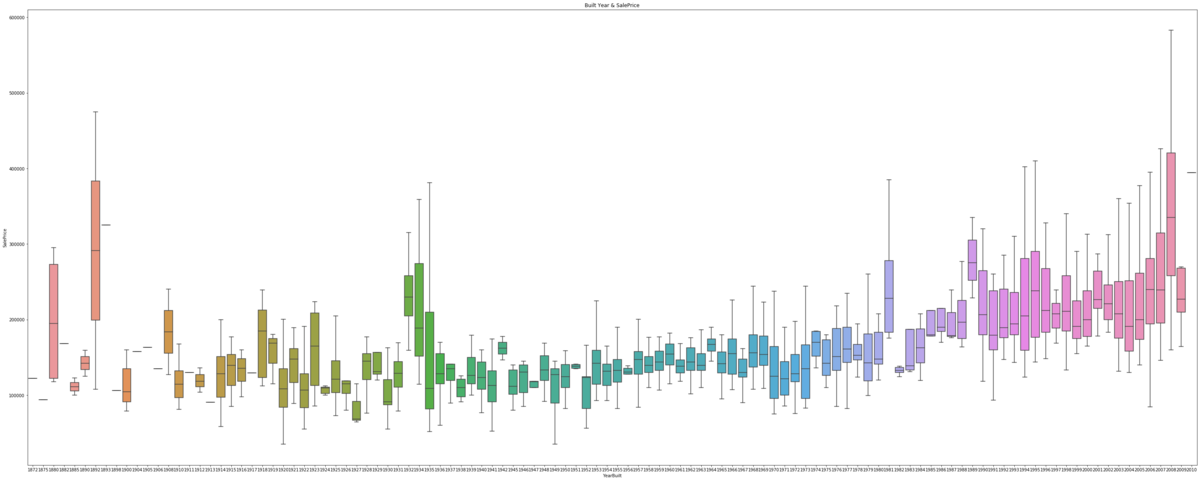
グラフをみると年内でのばらつきは大きいですが最近に近いほど住宅価格は高いことがわかります。（グラフのメモリが見にくくなってしまい申し訳ないですが横軸は右に行くほど最近の年代になります。）
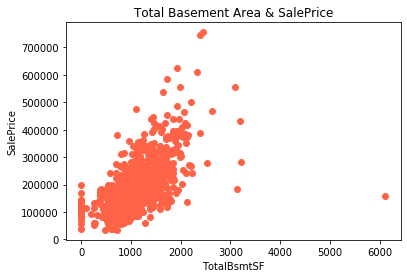
次に面積と品質についてみていきます。今回面積に関してはガレージの面積(’GarageArea’)と地下室全体の面積（’TotalBsmtSF’）を可視化してみました。
〈ガレージの面積と住宅価格〉

〈地下室全体の面積と住宅価格〉

〈全体の品質と住宅価格〉

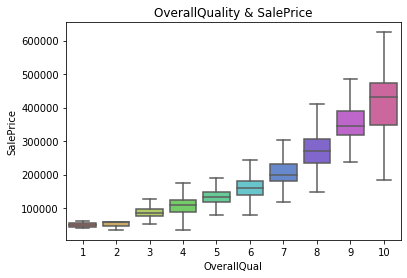
どちらも住宅価格と正の相関が見れそうです。僕らの感覚的にも広い家の方が値段が高いのはうなづけるような気がします。また全体の品質のランクが上がると住宅価格も応じて上昇していることもわかります。やっぱり質のいい広い家はどこも高いんですね。

残りの家の個々の設備とNeighborhoodについてもみていきます。
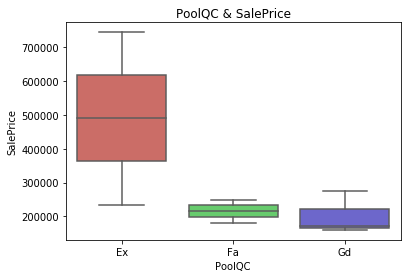
〈プールの品質と住宅価格〉

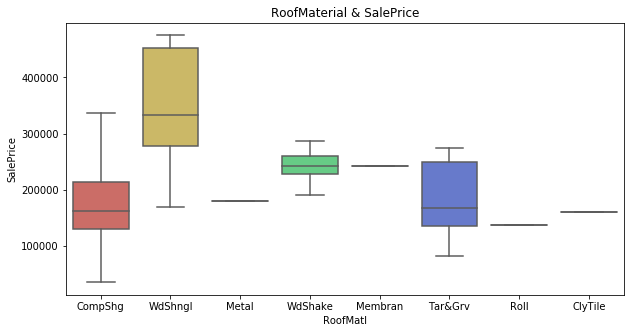
〈屋根の材質と住宅価格〉

〈 Neighborhoodと住宅価格〉

(15:NWAmes, 16:NoRidge, 22:StoneBr なんのこっちゃ)

さて、家の各設備の代表としてプールの品質と屋根の材質を見てみましたがどうやら特定の品質（PoolQCのEx、Extraのことだと思われます）とある材質（WdShngl、細かい説明がなかったので正確ではないですがWdがWoodぽい）だと住宅価格が高かったりするみたいですね。良い設備があったり、良い建築材使うと高いみたいです。
またNeighborhoodは一部で住宅価格が高かったりしました。ただ、調べてみましたがデータ名が略称でかつ説明が見当たらなかったのでこれに関しては本当に何を表しているのか謎でした。でも家の近くに便利なものがあれば住宅価格は高くなる気もします。

最初は変数が多すぎて戸惑いましたが、目的変数の住宅価格に影響しそうな説明変数に絞って再度データを分析していくといろんなことが見えてきました。
また、共線性の問題もあるので重回帰で使用した変数同士が強く相関してないか相関係数のヒートマップを作成してみました。

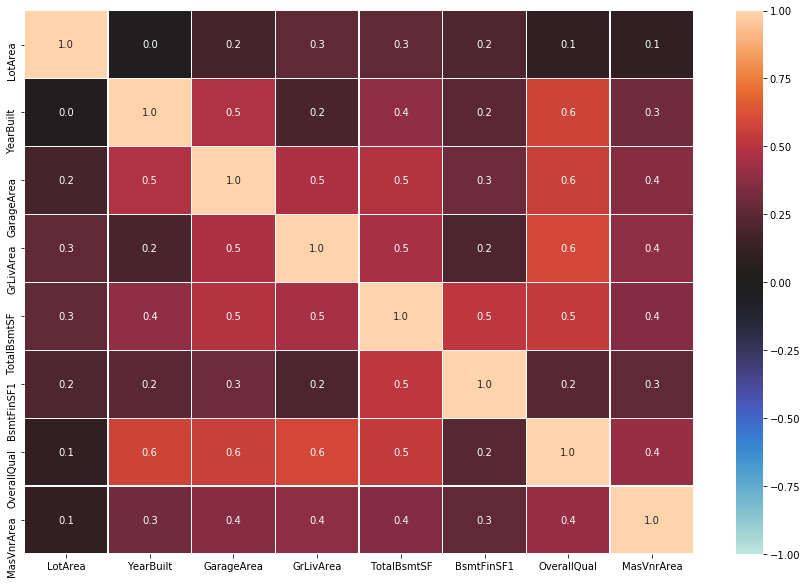
う〜ん、なんとも言えないくらいの相関です。本当はVIF等の指標も見るべきなのですが、モデルの精度的に今回はLightGBMRegressorを使用していくことにしたのでここで止めときます。

RMSEはダメ？
さて、いったんざっくりとモデルの構築と評価を行なったのでここで先輩社員の方に助言を求めました。するとこのような答えが返ってきました。
「大まかなところは大丈夫です。ただ、住宅価格のように下限があり、分布が偏る可能性があるデータのモデルの評価はRMSEでは本当はあまり良くないので調べといてください。」
このコメントをいただいて初めはイマイチピンときませんでしたが、この記事は僕らの学びの記事なので自分でも振り返れるように理由を書いていこうと思います。
まず、今回の住宅価格のデータの分布を見ていきます。

住宅価格などは原理的に０未満が存在せずに下限値が存在します。かつこのグラフの様に左右対象ではなく右に裾の長い分布になっています。
これの何がまずいかと言いますと、回帰モデルは目的関数として使用されるRMSE（平均平方二乗誤差）と呼ばれる以下の式を用いまして、（初めてブログで数式書きました。意外とすぐできるんですね。）

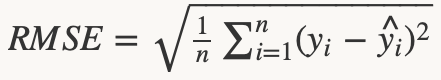
最小二乗法によって係数を推定し目的関数であるRMSEを最小化するのですが、RMSEを目的関数にするには残差が正規分布にしたがっていることが前提となります。
しかし今回のような分布では、そもそも下限があり裾が片方に長いため、残差も正規分布に従わないことが考えられます。（ここら辺の書き方厳密でなくて申し訳ないです。精進します。）
となると、残差が正規分布に従っていないことが考えられるのでRMSEを使用するのはあまり良くないことになります。（ただ、Kaggleでも多くの方はRMSEで評価されていたりします。）
この時の対処法としてわかったのが以下の3つです。
1：最尤法を用いて係数を推定してから当てはめを行う。
2：モデルに何らかの処理（対数をとる、平方をとるなど）を行い推定をする。
3：LightGBMRegressorではガンマ分布をeval_metricに設定できるので設定して行う
これ以外にも方法はあるみたいですが、まずは自分が理解が追いつくとこでこの3つをあげました。

アドバイスをいただいた後、個人的に以下の2つの方法に挑戦してみました。
1：目的変数に対数をとる。
2：LightGBMRegressor のeval_metricをgammaに設定する。
それではここから、それぞれの結果をみていきます。

アドバイスを元にいろいろしてみた結果
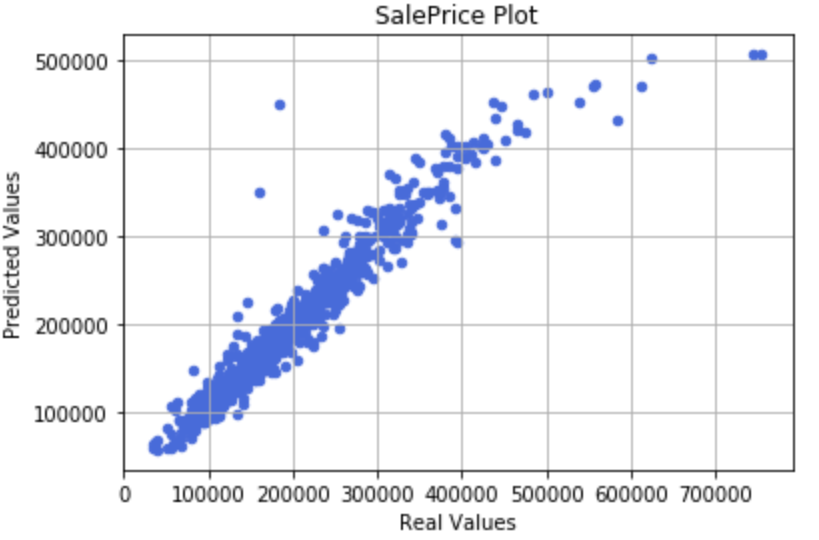
さて、これからアドバイスを元に修正を行なっていくのですが、違いがわかる方が良いので現時点での実際の住宅価格と、LightGBMRegressorでeval_metricをrmseに設定したモデルでの予測値をプロットして比較してみたいと思います。

では、プロットしてみたグラフが以下のようになります。

このプロットをみると低-中価格のところは正の相関がみれ正確に予測できていそうですがSalePrice が500000を超えたあたりから予測値は実測値を捉えきれず、実際よりも低い値段を予測してしまっています。
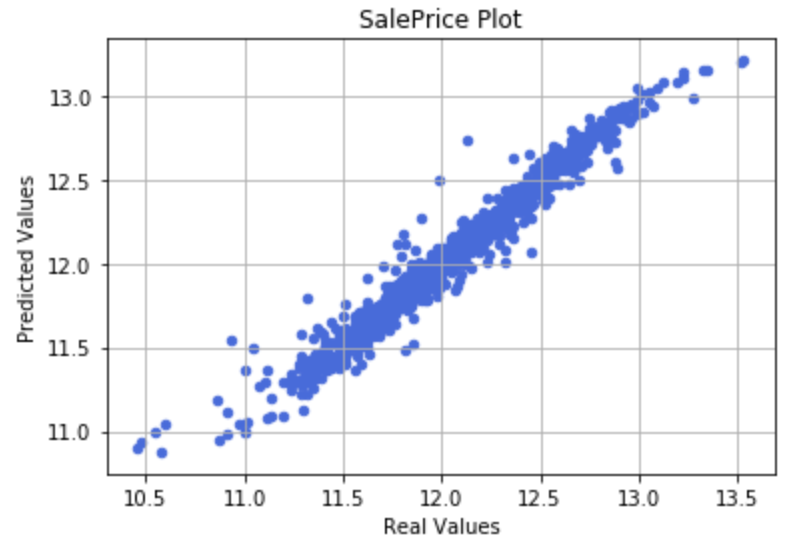
もっとはっきりと誤差があることを理解するために実測値から予測値を引いた残差をプロットしてみます。

残差プロットの真ん中に黒線を引いたのですが、高い価格帯において中央線からの残差の幅が広くなっていっていることがわかります。残差が正規分布に従うならここは広がらず一定となるはずです。

それではまず目的変数に対数をとり、精度がよくなるかどうかと予測値と実測値のプロット、また、残差プロットを作成して先ほどとの違いを見てみます。
まずコードを以下のように一部修正しました。

#上記のLightGBMRegressorのコードのうち変更した部分のみ表示
#目的変数に対数をとった
X_re = train_re.iloc[:,:-1]
y_re_log = np.log(train_re["SalePrice"])

scores_log = []
r2_scores_log = []

kf = KFold(n_splits=5, shuffle=True, random_state=0)
for tr_idx, va_idx in kf.split(X_re,y_re_log):
tr_x, va_x = X_re.iloc[tr_idx], X_re.iloc[va_idx]
tr_y, va_y = y_re_log.iloc[tr_idx], y_re_log.iloc[va_idx]

model_cv_log = lgb.LGBMRegressor(boosting_type='gbdt', num_leaves=31, max_depth=- 1, learning_rate=0.001, n_estimators=10000, subsample_for_bin=200000, objective=None, class_weight=None, min_split_gain=0.0, min_child_weight=0.001, min_child_samples=20, subsample=1.0, subsample_freq=0, colsample_bytree=1.0, reg_alpha=0.0, reg_lambda=0.0, random_state=None, n_jobs=- 1, silent=True, importance_type='gain')
model_cv_log.fit(tr_x, tr_y, eval_set=[(va_x, va_y)],eval_metric= "rmse", verbose = 1000, early_stopping_rounds = 200)
va_pred = model_cv_log.predict(va_x)
score = np.sqrt(mean_squared_error(va_y, va_pred))
scores_log.append(score)
score3 = r2_score(va_y, va_pred) 
r2_scores.append(score3)

目的変数に対数をとった結果、RMSEとR^2値は以下のようになりました。

RMSEは対数をとったため比較はできないですがR^2値においては少し当てはめの精度が良くなったみたいです。
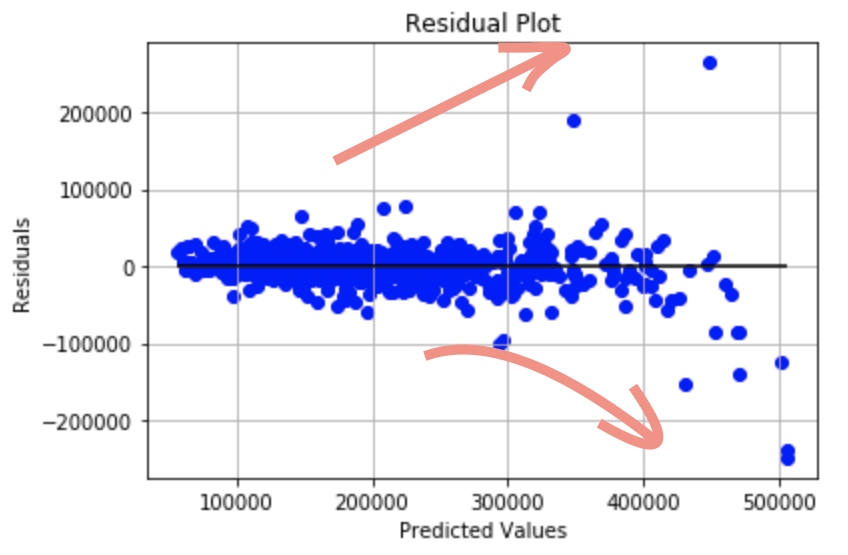
それでは実測値と予測値のプロットと残差プロットの結果です。

スケールが違ってしまい申し訳ないですが、先ほどと比較すると値が高いとこでの予測値のズレと広がりが軽減されています。

では次にLightGBMRegressorのeval_metricにgammaを設定した際の結果を示していきます。
まず、コードの一部を以下のように変更しました。

model_cv = lgb.LGBMRegressor(boosting_type='gbdt', num_leaves=31, max_depth=- 1, learning_rate=0.001, n_estimators=10000, subsample_for_bin=200000, objective=None, class_weight=None, min_split_gain=0.0, min_child_weight=0.001, min_child_samples=20, subsample=1.0, subsample_freq=0, colsample_bytree=1.0, reg_alpha=0.0, reg_lambda=0.0, random_state=None, n_jobs=- 1, silent=True, importance_type='gain')

#eval_metric= "gamma"に設定
model_cv.fit(tr_x, tr_y, eval_set=[(va_x, va_y)],eval_metric= "gamma", verbose = 1000, early_stopping_rounds = 200)

これを実行して得たRMSEとR^2値が以下の通りです。

結果はそこまでrmseと変わりませんでした。
予測値と実測値のプロット、残差プロットをみてみると

あまりrmseの時と変わっていない気がします。今回は目的変数に対数をとった方を採用することにしました。

さて一通り予定していたモデルの構築ができたので今回は目的変数に対数をとったLight GBMRegressorのモデルを使用してKaggleに結果を提出してみました。

ふむふむ大体半分くらいの順位になりました。もっと細かくパラメーターを調整したりニューラルネットワークなどを使用すれば精度を上げられる気がしますが、今回の研修は回帰モデルの基本的な組み方を学ぶことが目的なのでここまでとしました。ですが、年内か来年には本格的にKaggleに挑戦してみたい気持ちが自分の中で大きくなってきているので、個人かチームで挑戦してみようと思います。（参加してNotebookやDiscussionを読むだけでもかなり勉強になります。）

総括

今回の研修では構造化されたデータを使用して回帰分析のモデルを組む練習を行いました。個人的にはこのような感想を持ちました。

データセットが思ったよりも整っておらず、改めてクリーニングの計画を立てる重要性を感じた。
分類と違って回帰ではどの変数が目的変数に影響を与えるのかを調べるのが大変だった。
残差が正規分布に従っていないときなどのように条件によって使用できる関数やモデルが変わることを知った。
データの探索とモデルでの変数の評価を何回も行ったりきたりすることが大事なのがわかった。
ひたすらグラフを作ったのでMatplotlibライブラリでのグラフの可視化の実装が早くなった！
新卒への研修でどんなことを学ばせたいのか悩まれている方は参考にしてみてください！
では次回の記事もお楽しみに！