こんにちは。シニアデータアナリストの大前です。 大規模モデルの解析の新展開として二重降下とよばれる現象と理論について記事を書こうと思います。
二重降下の再現
大規模モデルの解析の新展開として二重降下とよばれる現象と理論があります。 この理論はデータ量が十分多いとき、
一定以上に過剰に増やされたパラメータは、逆に過学習を防ぐということを言っています。
論文 Two models of double descent for weak features (https://arxiv.org/abs/1903.07571) にその例が載っていますので、実際に再現してみました。
https://github.com/tohmae/double-descent-sample/blob/main/sample.ipynb
初期設定
D=200 train_num=80 #学習データの数 test_num=20 #テストデータの数 sigma = 1/5 #ノイズの標準偏差 b = 2 * np.random.rand(D) -1 b = b / np.linalg.norm(b) # β |β|=1
学習データ、テストデータ(x)
train_X = np.random.randn(train_num, D) test_X = np.random.randn(test_num,D)
学習データ、テストデータ(y)
train_y = np.matmul(train_X, b.T) + np.random.normal(0, sigma, train_num) test_y = np.matmul(test_X, b.T) + np.random.normal(0, sigma, test_num)
パラメータ数を制限した時のβの予測値
def calc_reg(param_num):
b_pred = np.linalg.lstsq(train_X[:,:param_num], train_y, rcond=None)[0]
return b_pred
予測パラメータ時のloss
def calc_loss(X, y, param_num, b_pred):
y_pred = np.matmul(X[:,:param_num], b_pred.T)
loss = np.sum(np.abs((y - y_pred)*2))/ len(y)
return loss
パラメータ数を変更した時の学習データおよびテストデータのloss
param_nums = []
train_losses = []
test_losses = []
for param_num in range(1,D+1):
b_pred = calc_reg(param_num)
train_loss = calc_loss(train_X, train_y, param_num, b_pred)
test_loss = calc_loss(test_X, test_y, param_num, b_pred)
param_nums.append(param_num)
train_losses.append(train_loss)
test_losses.append(test_loss)
可視化
import matplotlib.pyplot as plt
import japanize_matplotlib
fig, ax = plt.subplots(figsize=(8,8))
ax.plot(param_nums, train_losses, label="train")
ax.plot(param_nums, test_losses, label="test")
ax.set_xlabel('パラメータ数')
ax.set_ylabel('loss')
ax.legend(loc=0)
plt.ylim(-1,5)
fig.tight_layout()
plt.show()
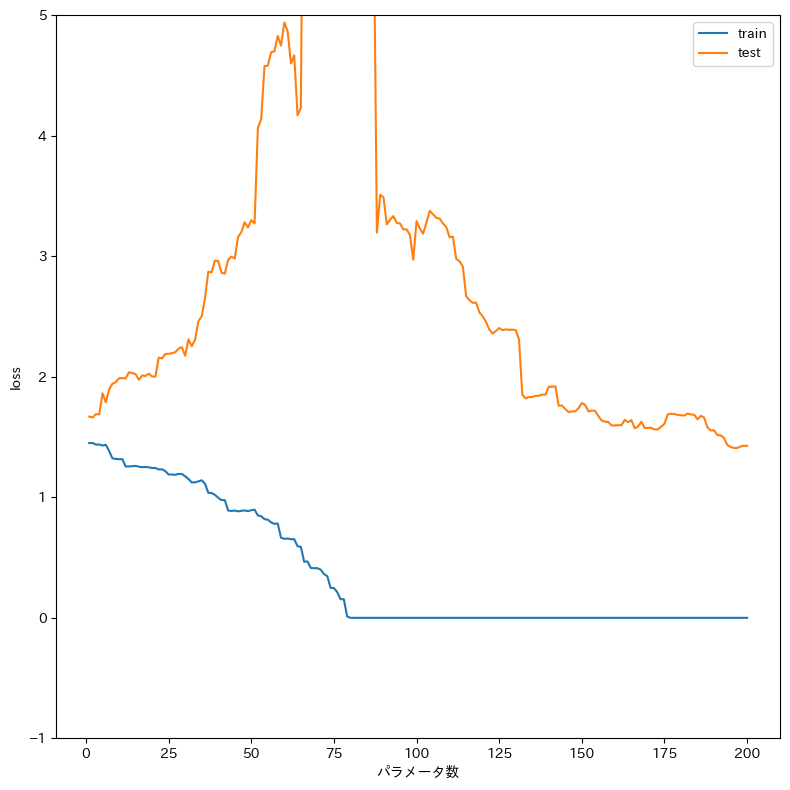
lossのグラフ
一度上がってしまった汎化誤差(testのloss)がパラメータをさらに増やすと下がっています。
再現は以上です。今回試したことによって自分の学びにも繋がりました。みなさんもぜひ試してみてください。
※2024年1月現在の情報です。

