
こんにちは! デジタルテクノロジー統括部に新卒入社した柳澤です。
研修中に得た学びを記録していきたいと思います。ちょっと、かなり、更新が遅れていますが。。。なにはともあれ、前回の記事↓の続きを書いていきます。
・予測モデル構築
さて、前回は環境構築のところのみで1回分使ってしまいましたが、今回からが本題です。Titanicのデータから、予測モデルの構築を行います。データサイエンスの界隈では非常に有名なコンペです。
今回は、まずデータの外観を把握して、のちに二種類の方法でモデルを構築します。その際には、データの前処理についても述べていき、最後に、それらが持つ精度を比較し、反省点などを記しておくことにします。また、少々余談ですが、そもそもTitanicってどういうデータなの?という部分について調べたため、そちらについても載せています。
・どんなデータか?
今回扱うデータはTitanic号が沈没した際の生存者と犠牲者に関するものです。このデータはkaggle上で提供されており、初心者用の課題としてポピュラーなものです。
・データの外観
このデータセットは次の変数からなっています。
PassengerID:乗客ID
Survived:生死 (1: 生存, 0: 死亡)
Pclass:客室の階級1→2→3
Name:名前
Sex:性別
Age:年齢
SibSp:兄弟姉妹、配偶者の数
Parch:両親、子供の数
Ticket:チケット番号
Fare:乗船料
Cabin:部屋番号
Embarked:乗船港
これらの変数のうち「Survived:生死」の変数に対して、その他の変数から予測をするようなモデルを構築するのが今回の目的です。
さて、今回の予測で重要なのは、「何が生存につながったか?」です。
Titanic号が事故に遭った際、救命ボートで避難するにあたって、女性や子供が優先されていたと言われています。なので、女性や子供の生存率が高い、等という仮説がたてられます。つまり、「その人がどういう属性の人だったか」ということを想像しながら分析をしていくことになります。
改めてこれらの変数をよく眺めると、生死以外の変数は次の三つに分類できます。
1.パーソナルなデータ
- PassengerID:乗客ID
- Name:名前
- Sex:性別
- Age:年齢
2.家族関係のデータ
- SibSp:兄弟姉妹、配偶者の数
- Parch:両親、子供の数
- 3.乗船した状況に関するデータ
Pclass:客室の階級1→2→3
- Ticket:チケット番号
- Fare:乗船料
- Cabin:部屋番号
- Embarked:乗船港
今回の場合は、年齢や性別などのパーソナルなデータが生存率に影響するものと考えられます。どうやら今回、欠損値があるのはAgeとFareであり、そのほかには欠損値がありません。ここで気にかかったことは、家族構成の変数、すなわちSibSpやParchについて、欠損値がないことです。これらについては、この記事の最後の部分で触れています。
さて、TicketやCabinについては、暗号のような数字の羅列になっています。
なんらかの手法を用いれば傾向が見えるとは思いますが、あまりここに時間をかけるのも得策に思えません。したがって、今回はTicketとCabinについては考慮せず、欠損値を処理しながらモデルを構築していくこととします。
・避難における男女の差、年齢の影響について
ここで、単純なデータ分析による考察を行います。それは、男女差や年齢が生存とどう関係していたか、についてです。これは、データを可視化し、全体的な傾向を捉えることで把握したいと思います。
まず、男女差については、男女別の生存率を棒グラフでプロットします。
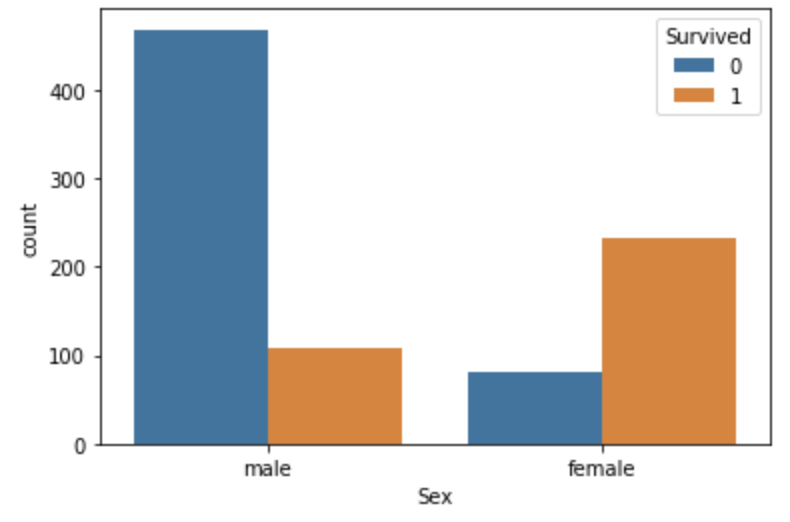
このように、女性の方が圧倒的に生存率が高いことがわかります。これは、避難の際に優先されたか否か、が大きく影響したことを示す結果です。また、年齢と生存率については、カーネル密度推定によるグラフを描くことで調べたいと思います。
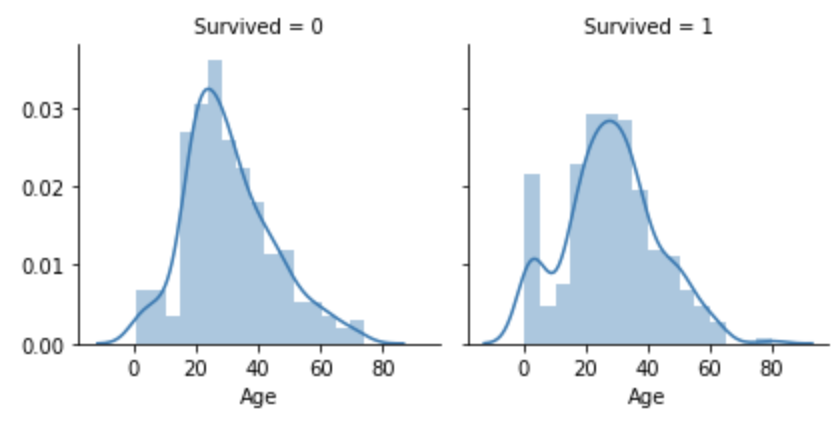
実線で描かれた部分が予測された分布であり、実戦から逸脱して多い量については特徴的なものといえます。ここでは、生存した側の分布において、0歳から5歳までの幼児の生存率が高いことが伺えます。このことから、幼児は特に優先して避難することができたといえそうです。
・処理の話。分析手法はなにか。
今回のように生存するかしないか、という二つの場合への予測は、分類問題と呼ばれます。分類問題に対する解法にも様々なものがありますが、ここで注目するべき手法にLightGBMがあります。回帰分析などの手法では、全ての説明変数が独立であることが求められる一方、決定木ではここを考慮する必要がないのも魅力です。とくにkaggleのコンテストなど、分類問題を解くにはこのLightGBMを用いるのが最もよいとされています。
さて、ここで、今回与えるデータには独立ではない関係を持つ変数が複数見られます。
このことからも、LightGBMが適していると考えられます。今回は勉強のため、ロジスティック回帰を利用した分析も行うこととします。
・LightGBM
さて、今回LightGBMを扱うにあたって、欠損値を埋める必要があります。この分析では、nan値に対して、ありえない数字(Age:-1など)をあてることとします。これは、外れ値に強いという特徴が決定木にあるためです。これらのデータに対して、scikit-learnを用いてモデル構築を実行していきます。
さて、LightGBMは決定木を一度の学習でいくつも作成しつつ、より良い結果になるよう改善していくアンサンブル機械学習の手法のひとつです。この手法を評価する指標の一つに、importanceがあります。このimportanceの高低により、今回構築したモデルにおいてどの特徴量(変数)が分類のために重要であるかを判断することができます。
今回の結果で得られたimportanceは次のようになります。
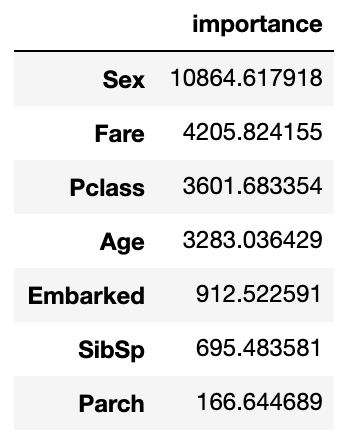
今回のlightGBMにおけるimportance(type='gain')からは、主に四つの変数が重要であったことがわかります。ここで、運賃と等級についてはかなり似た意味を持つ変数であると考えられますが、同じくらい重要であるという結果を示しています。もしかしたら、運賃は等級と異なる面で重要なのか? という点は気になるところです。
次に、モデルの評価のために精度(accuracy)、適合率(precision)、再現率(recall)、f値を出すことで評価していきます。この指標は、二種類(今回ならば生存かどうか)の予測結果が正しいかどうかを集計し、その結果から計算されるものです。集計した指標については真陽性、偽陽性などと呼ばれます。昨今お馴染みですね。予測の精度にとっては、それぞれの指標が全体的に高いことが望ましいとされています。
今回は、次のような値になりました。

また、同様に予測性能を評価するためにROC曲線もよく使われます。
こちらは真陽性率と偽陽性率から算出されています。
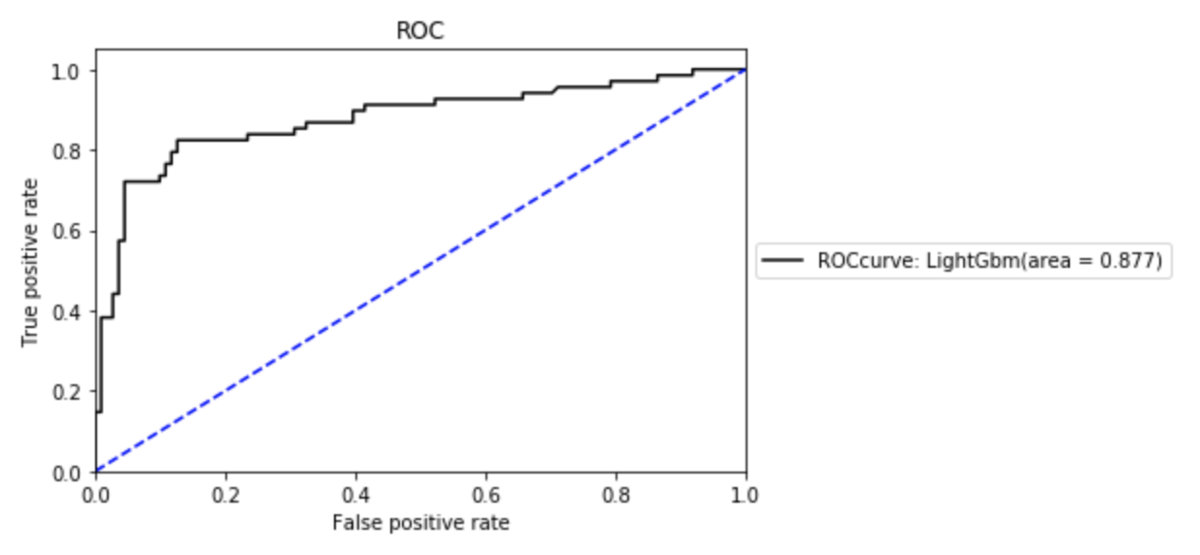
ここで、AUCという指標はこの曲線から下の面積の大きさであり、この面積の大きさで精度の高さを判断することができます。今回は、それなりの結果、ということのようです。
・ロジスティック回帰
さて、次はロジスティック回帰によるモデル構築を実施します。今回の場合は、説明変数の間に独立でない関係が混ざっている(船室の等級とチケット代など)と考えられますが、どの程度まで精度が高められるでしょうか。ここで、ロジスティック回帰の場合は外れ値に弱い特徴があります。したがって、今回は欠損値処理のやりかたを工夫してみました。今回行ったのは、ドロップ、平均値、hot-deckの三種類になります。
それぞれ、
ドロップ:欠損値を含む行全体を削除
平均値:その変数の平均値を代入
hot-deck:欠損値以外の変数が類似した行を見つけ、よく似た値と推定して欠損値に代入
今回は、hot-deckについてはKNN imputerを用いて推定しました。それぞれの場合の混同行列と指標は、次のようになります。



そして、これらを重ねて表示したROC曲線が次のようになります。
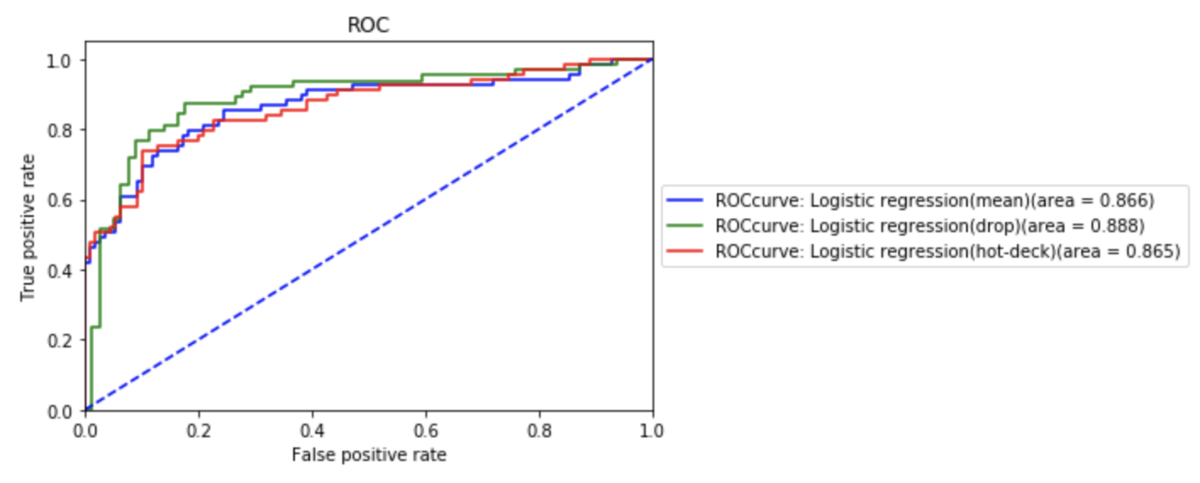
なんと、行削除がもっともよい成績のようです。行削除の難しい点は、絶対的に情報量が減ってしまうということです。この情報量をもったいないと感じるために、様々な欠損値処理が提案され使われています。今回の場合は、891人の乗客データから、実に177人分のデータを削除することになっています。かなりの情報量が減ってしまったはずです。本来ならば、もっと良いモデルを目指すために行う作業が、裏目に出たともいえます。
(実は、ここでは”やってはいけない比較”をしています。どこが妥当でないかについては、今後の記事で触れます!)
ここで、先ほどのLightGBMにおけるimportance同様、ロジスティック回帰の結果に対しても、どの変数が重要だったかを調べることができます。これは単純に回帰係数を見ていけばよいので、行削除を行ったものについて出力すると次のようになります。
coefficient [Pclass,Age,Sibsp,Parch,Fare,Sex,Embarked] = [-1.161, -0.051, -0.378, -0.053, 0.002, 2.476, -0.234]
intercept = [3.26876391]
今回、最も効いている変数はそれぞれ、性別、等級が主で、他にもSibspと寄港地の影響もありそうです。しかし、ここで重要なのは、年齢と運賃による影響が薄いという点です。この理由として、線形回帰の特徴が挙げられます。線形回帰モデルでは、得られた残差が正規分布に従うことを仮定しています。そのため、入力として与えるデータに関しても、正規分布に従うことが望ましいとされています。
今回扱った年齢と運賃について、それぞれヒストグラムを作ると次のようになります。
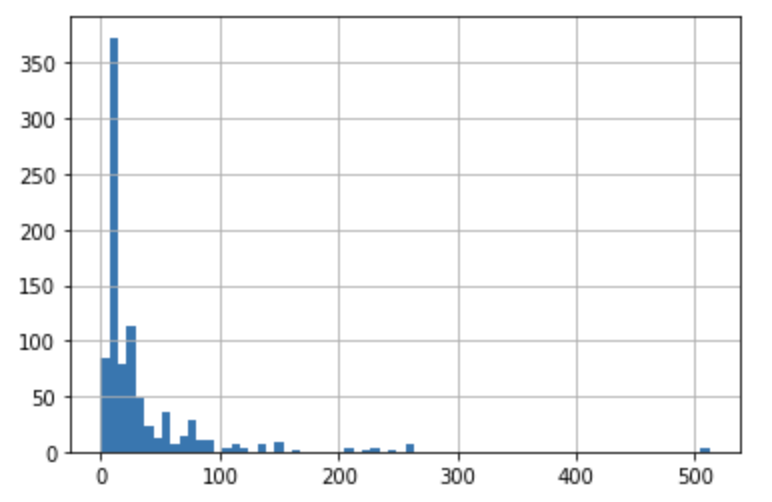
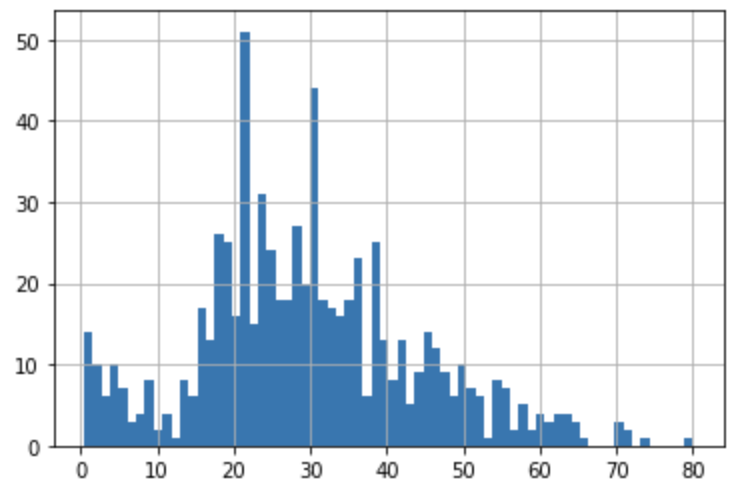
年齢については微妙ですが、運賃についてはかなり偏った分布になっています。もしかしたら、この辺りが原因かもしれません。考えられる対策としては、それぞれの値に閾値をもうけ離散値として扱うことでもう一度分析を実施することです。これによって、より良い精度を得ることができるかもしれません。また、LightGBMとロジスティック回帰の四つの場合を重ねたROC曲線は次のようになります。
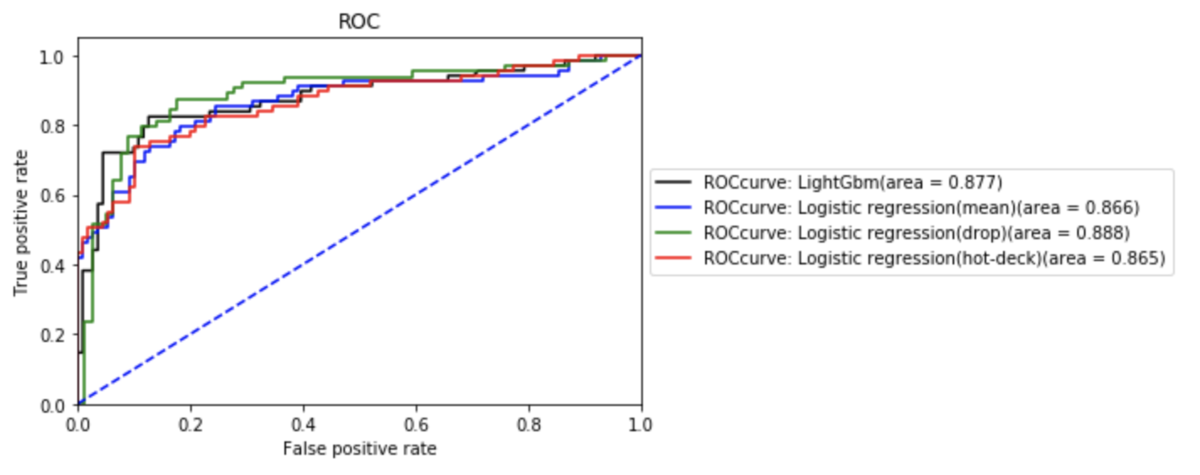
今回はそれぞれがAUCで0.865~0.888と、いずれも同様の曲線を描いていますが、LightGBMが最も良い結果を残しやすいはずと言われています。また、この中で行削除したものとLightGBMについてはkaggleにsubmitし、成績を出してみました。
それぞれ、
LightGBM: 0.76794
ロジスティック回帰(ドロップ):0.74641
となり、僅差でLightGBMのほうが良い成績に。
LightGBMのポテンシャルを引き出せていないのでしょうか?
より良い前処理や、チューニングの方法についても勉強していきたいと思います。
・このデータって結局なんなの?
さて、ここまでこのデータを用いて解析してきましたが、実は一番最初に疑問に思ったことがあります。そもそもSibSpやParchってなんなのでしょう?
兄弟や親子の関係に絞ってデータ化された、という点から、これはかなり特殊な用語だと思われます。この指標、どうやって調べたのでしょう?
Titanicに乗る人の気持ちになって考えてみるとわかりやすいかもしれません。冷静に考えれば、乗客名簿にこんな項目を書く欄は、おそらくないはずです。なにより、Ageには欠損値が生じているのに、SibSpとParchには欠損値が生じていないのがとても奇妙なことに思えます。チケットの番号を調べるのと同じように家族構成が調べられるとすれば、なぜ年齢が判明しないのでしょうか。
ここまで考えると、ここの値は、年齢不詳な人物などによる影響を必ず受けるはずではないか、と考えてしまいます。(ある人物の子供だと思っていたら兄弟だった、など)前提を疑う、というのはこれまでトレーニングしてきたことですが、考え始めたらどんどんと気になってきてしまいました。せっかくなので、データの出どころまで遡ってみることにします。
・データの出所。
まず、このSibSpという指標について簡単に調べましたが、残念ながら、どこを見てもTitanicの記事しか出てきません。データはkaggleからでてきたものですが、もちろんkaggleが用意したデータではありません。
もともとの出どころを色々な場所から探してみると、どうやらヴァンダービルト大学の生物統計学教室が提供するデータだということがわかりました。
このページでは、Titanicのデータだけでなく、様々なデータが用途フリーで置いてあります。さらにTitanicのデータに付属していたスクリプトをよく読み込んでいくと、encyclopedia Titanica というサイトから調査したものであることがわかりました。
そんなサイトがあるんだ、と思いながら開き、驚きました。
Titanicの事故を生き延びたあと、どのように暮らしていたか、また、どのような経緯で事故にあってしまったか、などがびっしり掲載されています。乗客ひとりひとりのドラマが凄まじい熱量で記載されております。
どうやら、Titanicのデータは、ここのプロフィールからひとりひとり家族関係を洗って、ヴァンダービルト大学のひとたちが頑張って作成したらしい、ということがわかってきました。また、このスクリプトを読み込むと、ひとつずつ調べたものだから抜け漏れがある、との断り書きも。これで疑問の大きな部分は解消しました。
こういった経緯で調査をしているということであれば、年齢は空欄でありながら、SibSpやParchなどの調査者が作成したと思しきデータに空欄がないことも、理解できます。
ただし、その分SibSpとParchの二項目に関しては、実際の数よりも少なくなる方向でバイアスが働いているといえそうです。もしかしたら、精度に影響が出ている可能性もあります。
・文献
一応、ついでなのでこれが使われた文献についても調べました。google scholarの検索機能で、2002年以前のものを検索。このホームページにデータセットが記載された以前の文献を調べてみると、出てきたのがこちら。
やはりというか、普通に教材でした。しかも、結構よく知られている本のよう。
言われてみればこのデータの取り方、いかにも演習の授業とか研究室の思いつき業務の予感がします。こちらの教材はspringerからダウンロードできるようです。(Covid-19の影響で、様々な書籍がフリーでダウンロードできるようになっています)。
Titanicのページでは、 ロジスティック回帰やノンパラメトリック分析、欠損値処理などが解説されています。どうやら、Titanicというコンペは、この教科書で勉強していた人たちが、懐かしのデータを使って初心者用として出題した、ということのようです。
・結局SibSpの出どころはわからなかった
さて、こちらの教材でもSibSpとParchを用いた分析が行われていますが、やはりSibSpという用語の出どころはわかりませんでした。
そこで、もう一息Google Scholarなどで調べてみたところ、社会学系で同様の表現を用いた分析が行われた研究を複数見つけることができました。
しかし、流石にバックグラウンドがなく、解釈が難しいためここで追うのを諦めます。
ただし、分析のバックグラウンドを知っていく過程で、関連した分野でよく利用される指標などを知ることはできました。
たとえば、目を通した論文ではFamilysizeという指標が使われていました。この指標を導入して行う分析法は、kaggleではメジャーであり、予測に大きく貢献するようです。
非常に周りくどいやり方でしたが、このようにデータ分析にドメイン知識が役立つ理由を実感できた気がしています。
・教訓
【突っ込みすぎると歯止めが効かないので、注意しましょう】
Why 効率をよくしたい
少し、余計なところに首を突っ込んだきらいがあります。
結果的には、自分なりの学びを得ることができたのですが、基本的には迷走していた時間が結構ありました。
How 疑問にも優先順位を付けていく
まず、サクッと終わらせる癖をつけていきたいです。
興味の赴くままに熱中するのは楽しいのですが、ちょっとよくないな、と実感しています(原稿も延び延びに遅れるのでサイアクです)。
片付けるべき疑問にも、優先順位をつけていこうと思います。
・今回の反省点
最後に少し反省点。
今回、地味に強く感じているのは、pythonで苦労している部分が多い、ということです。Pandasとnumpyも含め、ほとんど触ったことがないレベルだったため、苦労してしまいました。頭の中では、この分析をやってみたい、と思いつつ、うまく実装できなかった部分があります。たとえば、scikit-learnを使うときには公式ドキュメントを眺めるようにしたいと思っていますが、例として挙げられているコードをどう応用すればいいか、がパッと思い浮かびません。結局どうすればいいかわからなかった、という方法も今回の場合は複数ありました。
経験不足以前に、知識不足が問題だと改めて痛感しました。この辺り、並行して補っていきたいです。意識して学習を続けていきたいと思います。

柳澤 寛光 Hiromitsu Yanagisawa
デジタルテクノロジー統括部 データ&テクノロジー ソリューション部 アナリティクスグループ
※2020年9月現在の情報です。
