文章中の誤植パターンを検知する。

技術 データサイエンス 文字列処理 アルゴリズム NLP デジタルテクノロジー統括部 pickup

トップ画像

はじめに

"シュミレーション"。理工系の方なら おそらくご存知のこの単語。
ゼミ発表時に 誤ってこいつを使うと 教官から "趣味レーション"などと揶揄され、「"Simulation"なのだから "シミュレーション"と表記するのが正しい」などの指導を頂くことの多い 誤表記 "シュミレーション"。
もしくは、これに限らず 文章中における TYPOや誤植パターンなどの検知について考察したいと思います。

 

もし、誤植のパターンが 予め分かっているのなら、文字列検索で早々に探してしまう戦略は"あり"でしょう。 

ex. grep シュミレーション target_file.txt

 

今回は一見すると見落としそうな または 表記における多様な"ゆれ"(とそれに伴う誤植)を対象に、これらを うまく検知し、あわよくば "表記ゆれ"コーパスなどにまとめて、文章作成の効率化を図れないか?など色々なことを考えているため、少し汎用的な誤植の検知を目指しました。

 

しかし、
例えば 形式言語の人ならば、有限長の文字列による有限パターンは正規言語となるので、(頑張れば)正規表現での記述が可能なのだからと、正規表現での記述パターンを編み出すのも理解はできるのですが、それほど簡単にコトが進むとは思えません。(単に、私が正規表現をそれほど得意としていないだけかも 知れませんが...)

例えば  文字列検索の人ならば、接尾辞配列(= Suffix Array)を作成し、比較を行うことで文字列の一致する部分を拾い集め、結果 似た文字列を探し出すと考えるかもしれませんが、できればメモリをもう少し小さく使って、効率よく処理できないかな? という欲もあったりします。

というようなことをつらつら考えながら、上記 TYPOや誤植 検出のためのプログラムを書いた際に参考にしたアルゴリズムなどについて ご紹介したいと思います。

 

Dot matrix plot

まず最初に思いついたのは 1970年 Adrian J. Gibbs らによる "The diagram, a method for comparing sequences. (Eur. J. Biochem 16: 1-11p)" で紹介された "Dot-matrix analysis" または "Dot-Plot" 。

この方法は、配列の類似性をざっくり見るのに、とても直感的で優れた手法だと思います。

 

手法における考え方は とてもシンプルで、

  1.  比較元となる m文字配列seq1 と比較先となる n文字配列seq2 に対して、2値(bool型)のm×nの行列Mを作成し(各成分の初期値は0=Falseとする)
  2. seq1 の i番目の文字と(1≦i≦m)、seq2 の j番目の文字と(1≦j≦n)が同じだった場合、成分 mijを 1=True とする。
  3. seq1とseq2のすべての文字を比較し、出来上がった行列 Mに対して、0の箇所は空欄に、1の箇所にドットを打てば 斜めの線上に おおよそ似通った文字配列の跡が映し出されます。

f:id:yyt2:20210629215116p:plain

図1-1. Dot matrix plot による "シュミレーション" の評価結果.

この斜めの線上に並んだドットが長ければ長いほど 互いの文字配列は似通っていることが分かり、ドットのある配列の対応部位長 と それぞれの元の文字配列長(m文字)とを比較することで 誤植の可能性を検知できるといった寸法です。 

 

Alignment

Dot matrix plot は、表示された ドットの表示図から、一見して異なる2つの配列の同じ部位の長さや状況を俯瞰的に把握するのに優れていますが、

  1. 似通った領域の文字配列長
  2. 誤植と思われる領域を含む 文字配列の開始部位と終端部位の把握

について、すぐに読み取ることは出来ません。

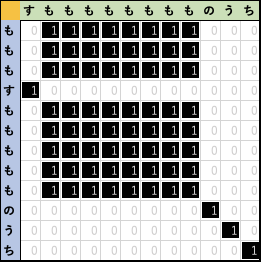
f:id:yyt2:20210629222332p:plain

図2-1. 一見して誤植部位を含む領域の文字配列長が読み取れない例.

今回、検知対象の TYPOや誤植パターンについて おおよそ以下の3種類のミスを想定しています。

  1. 異なる文字を打ち間違えた場合。(変異): ex. シュミレーション
  2. 文字入力が不足した場合。(欠失): ex. シミレーション
  3. 入力した文字が多すぎた場合。(誤挿入): シュミュレーション

このようなエラーが派生した箇所を比較できるように、比較元と比較先の文字配列の対応領域を特定できるように うまく並べたものを alignment と言います。

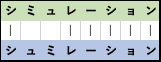
f:id:yyt2:20210703225206p:plain

図2-2. alignment の例(同じ文字の対応のあるものは "|" が表記されている).

このalignment表記により、比較文字配列同士が どれほど似通っているのか、見て取ることができます。

 

また、上記の欠損や誤挿入の場合、そもそもの文字配列の長さが異なり対応が うまく表記出来ません。このような長さ調整をするために、文字 "-" を挿入し対応のズレを補正します。これをgapと呼びます。

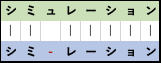
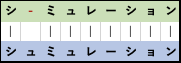
f:id:yyt2:20210704095031p:plain f:id:yyt2:20210704095206p:plain

図2-3. alignment におけるgapの例(対応づけのために "-" で伸長されている).

Alignment にも、個々の文字配列を1対1で評価する ペアワイズな alignment と、複数の文字配列を一気に比較してTYPOなどによる文字配列の進化的変化過程を読み解く マルチプルな alignment があります。

 

ここでは ペアワイズな alignmentを うまく求める手法について考えたいと思います。

 

Dot matrix plot を改良する1 (または gapを考慮しない alignmentの作成に向けて)

先の "dot-matrix plot"は、直感的にわかりやすいのですが、具体的な情報を得るのに いくつかの不満がありましたので、改良したいと思います。

 

まず、"似通った領域の文字配列長"が一見しても分かり辛い ことへの対処をしましょう。

 

基本的なアイデア 1: 

Dot-matrix plotで用いた行列は、その成分で ドットを表記するかどうかの情報のみを保持する 2値の行列でした。

しかし、先頭から連続的に対応している文字配列の長さを行列の成分に記録させれば、文字配列の対応状況にもう少し見通しがつくようになりそうです。

 

具体的には、

  1.  比較元となる m文字配列seq1 と比較先となる n文字配列seq2 に対して、整数(int型)のm×nの行列Mを作成し(各成分の初期値は0とする)
  2. seq1 の i番目の文字と(1≦i≦m)、seq2 の j番目の文字と(1≦j≦n)が同じだった(matchした)場合、成分 mij に 成分mi-1 j-1の値に+1した値を代入します。
  3. seq1とseq2のすべての文字を比較し、出来上がった行列 M中の各成分から最大値を持つ部位を求めます。

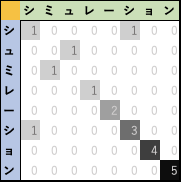
>f:id:yyt2:20210703231615p:plain

図3-1. 比較によって5文字の連続した同じ文字の列を持つ例.

この方法により、おおよそ似通った領域がどの辺りかを見通すことができそうです。

 

しかし、欲を言えば  "シミュレーション" ではなく、"シミュレーション" まで alignmentとして 欲しいので、その辺についてもう少し改良したいと思います。

 

基本的なアイデア 2: 

先の方法では、matchした部分への評価が行なわれていますが、matchしない つまりmismatch 部分についての評価が行われず、結果 文字配列中の TYPO の部分の情報がすっかり抜け落ちているように見受けられます。

なので、mismatch の評価も行うように改良しましょう。

 

具体的には、

  1.  比較元となる m文字配列seq1 と比較先となる n文字配列seq2 に対して、整数(int型)のm×nの行列Mを作成し(各成分の初期値は0とする)
  2. seq1 の i番目の文字と(1≦i≦m)、seq2 の j番目の文字と(1≦j≦n)が同じだった(matchした)場合には、成分 mij に mi-1 j-1+1 の値を、同じでない(mismatchの)場合には、成分 mij に mi-1 j-1-1 の値を代入します。
  3. seq1とseq2のすべての文字を比較し、出来上がった行列 M中の各成分から最大値を持つ部位を求めます。
  4. 最大値のある部位から左上/左/上方向の各成分を評価し、しかるべき場所までトレースバックできれば alignmentが求められそう?

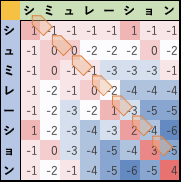
f:id:yyt2:20210704010739p:plain

図3-2. 比較によって得られた 連続した最長文字列箇所から alignment を取得しようとする.

と言う訳で、ある程度の方向性は見えそうなんですが、トレースバック条件についての考察が必要なところで 詰まりました。

 

また、トレースバックをするにしても gapとの絡みも考慮しないといけなさそうなので、次は gapに関する考察を行いたいと思います。

 

 Dot matrix plot を改良する2 (または gapを考慮する)

TYPOや誤植パターンのケースとして

  1. 異なる文字を打ち間違えた場合。(変異)
  2. 文字入力が不足した場合。(欠失)
  3. 入力した文字が多すぎた場合。(誤挿入)

を挙げました。

このうち gap が発生するのは "欠失"と"誤挿入"の場合で、それぞれの場合における dot-matrix plot の結果を表します。

 

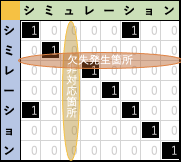
f:id:yyt2:20210704093617p:plainf:id:yyt2:20210704095031p:plain

図4-1. "欠失"を含む文字配列の dot matrix plot とalignment.

f:id:yyt2:20210704093713p:plainf:id:yyt2:20210704095206p:plain

図4-2. "誤挿入"を含む文字配列の dot matrix plot とalignment.

 

基本的なアイデア 3: 

Dot matrix plotは、対角成分上に連続して表示されるドットによって文字配列の対応具合が見て取れました。

今 考慮している gap が含まれる場合、ドットは 右/下 隣の成分にシフトしていることが分かります。

そこで、gap に関する評価も行うように改良しましょう。

 

具体的には、

  1.  比較元となる m文字配列seq1 と比較先となる n文字配列seq2 に対して、整数(int型)のm×nの行列Mを作成し(各成分の初期値は0とする)
  2. seq1 の i番目の文字と(1≦i≦m)、seq2 の j番目の文字と(1≦j≦n)が同じだった(matchした)場合には、成分 mij に mi-1 j-1+1 の値を、同じでない(mismatchの)場合には、成分 mij に mi-1 j-1-1 の値を代入します。
  3. "欠失"の可能性を考慮し、成分 mij の値が mi-1 j-1 より小さい場合には、成分 mij に mi-1 j-1 の値を代入します。
  4. "誤挿入"の可能性を考慮し、成分 mij の値が mi j-1-1 より小さい場合には、成分 mij に mi j-1-1 の値を代入します。
  5. seq1とseq2のすべての文字を比較し、出来上がった行列 M中の各成分から最大値を持つ部位を求めます。
  6. 最大値のある部位から左上/左/上方向の各成分を評価し、3方向成分の中で 値の大きな向きにトレースバックできれば alignmentが求められそう?

 

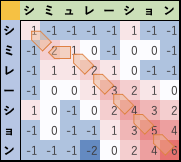
f:id:yyt2:20210704133409p:plain

図4-3. "欠失"を含む文字配列の alignment 予測状況.

 

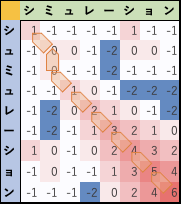
f:id:yyt2:20210704134404p:plain

図4-4.  "誤挿入"を含む文字配列のalignment 予測状況.

 

アイデアの修正: 

"欠失/誤挿入"を含む文字配列をトレースバックする様子を見るに、

  • 左方向へのシフトが起きる際は "欠損" による gapが発生し
  • 上方向へのシフトが起きる際は "誤挿入" による gapが発生している

ように 見受けられます。

この特徴を用いて、alignment作成方法をまとめると、 

  • seq1とseq2のすべての文字を比較し、出来上がった行列 M中の各成分から最大値を持つ部位を求めます。
  • 最大値のある部位から左上/左/上方向の各成分を評価し、3方向成分の中で 値の大きな向きにトレースバックするのですが、

 

より具体的には、

  • 比較元となる m文字配列seq1 と比較先となる n文字配列seq2の対応文字を抽出し、alignment用配列にそれぞれ格納する。
  • トレースバックの際、左方向へのシフトが起きたら、"欠損" が発生しているため比較先文字配列に gap文字 "-" を挿入する。
  • トレースバックの際、上方向へのシフトが起きたら、"誤挿入" が発生しているため比較元文字配列に gap文字 "-" を挿入する。

以上で、alignment の準備ができました。

 

Global alignment

これまでのアイデアは、1970年 Saul B. Needleman と Christian D. Wunsch による "A general method applicable to the search for similarities in the amino acid sequence of two proteins. (J. Mol. Biol. 48: 443-453p)" にまとめられています。

この論文で紹介されている 動的計画法によるアルゴリズム (Needleman-Wunsch アルゴリズム等と呼ばれます)は、gap を含む alignment を高速に取得するスマートな方法で、aligment 作成の前処理でも おおよそ O(mn)の計算量で済むほどです。

 

細かいことを言えば(すでにお気づきの方も多いと思いますが)、この処理は有向グラフの最適経路問題で、alignment 生成のための探索経路用の重みつきグラフを作成し、バックトレース時にはDijkstra法よろしく最適経路を選ぶことによって スマートに結果を得ることができていると言う訳です。

 

 

 では 先の論文の手法紹介も兼ね、TYPO検知のアルゴリズムをまとめます。

  1.  比較元となる m文字配列seq1 と比較先となる n文字配列seq2 に対して、整数(int型)の(m+1)×(n+1)の行列Mを作成する。(各成分の初期値は0とする)

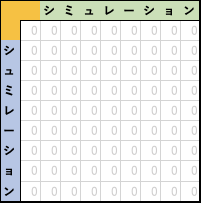
    f:id:yyt2:20210704150331p:plain

    図6-1. 行列の作成
  2. 配列長を正しく求められるように、それぞれの文字配列開始点に重みを設定する。具体的には、成分 m1j=-j+1, 成分mi1=-i+1 で文字配列開始点の初期化を行う。

    f:id:yyt2:20210704150433p:plain

    図6-2. 開始点の初期化
  3. 2×2の評価行列 

    f:id:yyt2:20210704152936p:plainを用いて残り成分の評価を行う。

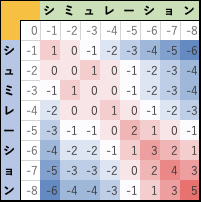
    f:id:yyt2:20210704154336p:plain

    図6-3. 各成分の評価.
  4. すべての文字を比較し、出来上がった行列 M中の各成分から最大値を持つ部位を求めます。(ここに関しては、Needleman-Wunsch アルゴリズムと異なり global alinment を求めていません!!)

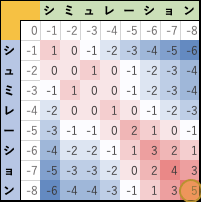
    f:id:yyt2:20210704155202p:plain

    図6-4. 最大値を持つ部位を求める.
  5. 最大値のある部位から左上/左/上方向の各成分を評価し、3方向成分の中で 値の大きな向きに(但し、3方向全て同じ値なら左上に)トレースバックを行います。

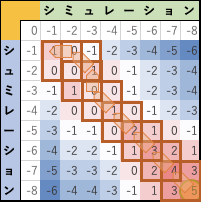
    f:id:yyt2:20210704160304p:plain

    図6-5. トレースバックの様子.
  6. トレースバックの経路に従いseq1, seq2 の対応文字列を生成します。但し、左方向へのシフトが起きたら 比較先文字配列seq1 相当配列に、上方向へのシフトが起きたら 比較元文字配列seq2 相当配列に gap文字 "-" を挿入する。
  7. 作成された配列を並べ alignment 情報を完成する。 

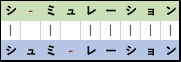
    f:id:yyt2:20210704161421p:plain

    図6-6. 作成された alignment.

 

まとめ

alignment によってTYPOなどによる 似通った文字配列領域の抽出を行うことができました。

 

しかし、それぞれの文字列比較に対して毎回 O(mn)の計算量がかかるので、処理自体はそこそこの重さがあります。

できれば、これより TYPOの発生確率を個別に計算しヒューリスティックな手法で もう少し処理の高速化を図れればと考えています。

f:id:yyt2:20210705212004j:plain

yyt2

デジタルテクノロジー統括部 デジタルビジネス部 アナリティクスグループ リードデータアナリスト

娘に振り回されっぱなしの毎日です。

※2021年7月現在の情報です。